Question

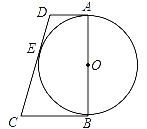
【题目】如图，在菱形ABCD中，过点C作CE⊥BC交对角线BD于点E，且DE=CE，若，则DE=_____.

Answer 1

【答案】1

【解析】

根据菱形的性质得出BC=CD=AB=，从而得出∠DBC=∠CDB，根据DE=CE得出∠CDB=∠ECD，得出∠DBC=∠CDB=∠ECD，根据三角形的内角和定理，求出∠DBC＝30°，再根据锐角三角函数求出CE的长即可。

解：在菱形ABCD中，BC=CD=AB=，
∴∠DBC=∠CDB，

∵DE=CE，∴∠CDB=∠ECD，

∴∠DBC=∠CDB=∠ECD，

∵CE⊥BC，∴∠BCE=90°，
在BCD中，

∠DBC+∠CDB+∠BCE+∠ECD=180°

∴∠DBC＝30°，
在RtBCE中，BC=

tan∠DBC= tan30°==
∴CE=1,∴DE=1

故答案为：1