题目内容
【题目】如图,在△ABC中,AB=AC=2,点P在BC上.若点P为BC的中点,则m=AP2+BPPC的值为多少?若BC边上有100个不同的点P1,P2,…,P100,且mi=APi2+BPiPiC(i=1,2,…,100),则m=m1+m2+…+m100 的值为多少?

【答案】4,400.
【解析】
第一个空,由等腰三角形的三线合一性质和勾股定理得出AP2+BP2=AB2即可;第二个空,作AD⊥BC于D.根据勾股定理,得APi2=AD2+DPi2=AD2+(BD﹣BPi)2=AD2+BD2﹣2BDBPi+BPi2,PiBPiC=PiB(BC﹣PiB)=2BDBPi﹣BPi2,从而求得m1=AD2+BD2=AB2,即可求解.
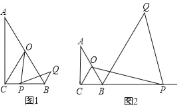
解:若点P为BC的中点,如图1所示:
AB=AC=2,
∴AP⊥BC,BP=CP,
∴∠APB=90°,
∴AP2+BPPC=AP2+BP2=AB2=4.
若BC边上有100个不同的点P1,P2,…,P100,
作AD⊥BC于D,则BC=2BD=2CD,如图2所示.
根据勾股定理,得
APi2=AD2+DPi2=AD2+(BD﹣BPi)2=AD2+BD2﹣2BDBPi+BPi2,
又∵PiBPiC=PiB(BC﹣PiB)=2BDBPi﹣BPi2,
∴m1=AD2+BD2=AB2=4,
∴m1+m2+…+m100=4×100=400.
故答案为:4,400.

练习册系列答案
相关题目