Question

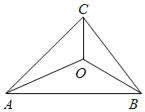
【题目】如图，已知等腰三角形ABC，CA＝CB＝6cm，AB＝8cm，点O为△ABC内一点（点O不在△ABC边界上）．请你运用图形旋转和“两点之间线段最短”等数学知识、方法，求出OA+OB+OC的最小值为_____．

Answer 1

【答案】4+2.

【解析】

以AB为边作等边三角形△ABD，以OB为边作等边△OBE．连接CD交AB于M点，可证△ABO≌△DBE，可得AO＝DE，则AO+BO+CO＝CO+OE+DE，即当D、E、O、C四点共线时，AO+BO+CO值最小，最小值为CD的长度，根据勾股定理求CD的长度，即可求OA+OB+OC的最小值．

如图：以AB为边作等边三角形△ABD，以OB为边作等边△OBE．连接CD交AB于M点．

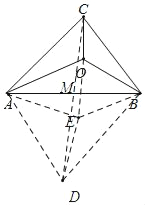
∵△ABD和△OBE是等边三角形

∴OE＝OB＝BE，∠ABD＝∠OBE＝60°，AB＝BD

∴∠ABO＝∠DBE且AB＝BD，BO＝BE

∴△ABO≌△DBE

∴AO＝DE

∴AO+BO+CO＝DE+OE+CO

∴当D、E、O、C四点共线时，AO+BO+CO值最小，

∵AC＝BC，AD＝BD

∴CD是AB的垂直平分线

∴AB⊥CD，AM＝MB＝4

∵CA＝CB＝6，AD＝BD＝8

∴CM＝2，MD＝4

∴CD＝4+2

∴AO+BO+CO最小值为4+2，

故答案为4+2，