题目内容
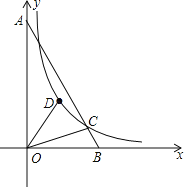
【题目】如图，一次函数
与反比例函数
的图象在第一象限交于A，B两点，A点的坐标为
，B点的坐标为
，连接
，过B作
轴，垂足为C．
（1）求一次函数和反比例函数的表达式；
（2）在射线
上是否存在一点D，使得
是直角三角形，求出所有可能的D点坐标．
【答案】（1）
，y＝
；（2）（19，3）或（
，3）．
【解析】
（1）先利用待定系数法求出反比例函数解析式，进而确定出点A的坐标，再用待定系数法即可求出一次函数解析式；
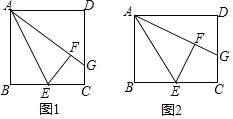
（2）由于点D在射线CB上，所以∠AOD≠90°，当∠OAD＝90°时，先求得直线AD的解析式，进而可求得点D坐标；当∠ODA＝90°时，设AO、BC交于点F，如图2，则易知DF＝
，求出点F的坐标和AO的长即可解决问题.
解：（1）∵点B（2，3）在反比例函数
的图象上，∴a＝2×3＝6，
∴反比例函数的表达式为y＝，
∵点A的纵坐标为6，点A在反比例函数y＝图象上，∴A（1，6），
把点A（1，6）、B（2，3）代入
中，得：
，解得：
，
∴一次函数的表达式为；
（2）由于点D在射线CB上，所以∠AOD≠90°.
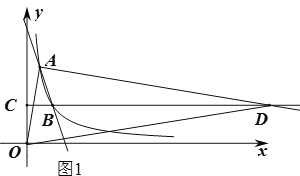
①当∠OAD＝90°时，如图1，∵直线OA的解析式为：
，∴设直线AD的解析式为
，
把点A（1，6）代入，得
，∴直线AD的解析式为
，
当y＝3时，x＝19，∴D（19，3）；
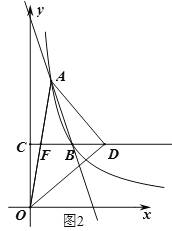
②当∠ODA＝90°时，设AO、BC交于点F，如图2，
∵A（1，6），B（2，3），
轴，
∴AF＝OF＝DF＝
，F（
，3），
∴点D的坐标为（，3）；
综上所述，满足条件的点D坐标为（19，3）或（，3）．
练习册系列答案
相关题目
