题目内容
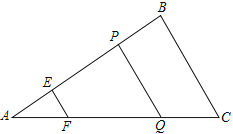
【题目】如图1,点A在第一象限,![]() 轴于B点,连结
轴于B点,连结![]() ,将
,将![]() 折叠,使
折叠,使![]() 点落在x轴上,折痕交
点落在x轴上,折痕交![]() 边于D点,交斜边
边于D点,交斜边![]() 于E点,(1)若A点的坐标为
于E点,(1)若A点的坐标为![]() ,当
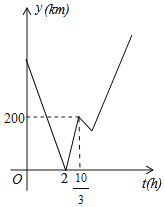
,当![]() 时,点
时,点![]() 的坐标是______;(2)若
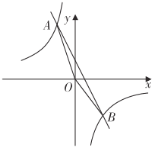
的坐标是______;(2)若![]() 与原点O重合,
与原点O重合,![]() ,双曲线
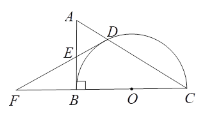
,双曲线![]() 的图象恰好经过D,E两点(如图2),则
的图象恰好经过D,E两点(如图2),则![]() ____.
____.

【答案】(![]() ,0)
,0) ![]()
【解析】
(1)由题意可求得OA的长,再根据三角函数与折叠的性质可得AE:OE的值,进而可求得AE与OE的长,然后由勾股定理求得OA′的长即得答案;
(2)首先设点A的坐标为(2a,2b),进而可表示出点E和点D的坐标,然后在Rt△OBD和Rt△OAB中,利用勾股定理可得关于a、b的方程组,解方程组即可求出a、b的值,进而可得结果.
解:(1)∵AB⊥x轴,A点的坐标为(4,3),∴OB=4,AB=3,∴OA=![]() ,
,
∵EA′∥AB,∴EA′⊥x轴,∴sin∠AOB=![]() ,
,
由折叠的性质可得:A′E=AE,∴AE:OE=3:5,
∴A′E=AE=![]() ,OE=
,OE=![]() ,
,
∴![]() ,
,
∴点A′的坐标是:(![]() ,0);
,0);
(2)设点A的坐标为:(2a,2b),
∵A′与原点O重合,∴点E的坐标为:(a,b),
∵双曲线![]() 的图象恰好经过D、E两点,∴k=ab,
的图象恰好经过D、E两点,∴k=ab,
∴点D的坐标为:(2a,![]() b),
b),
∴AB=2b,BD=![]() b,OB=2a,
b,OB=2a,
由折叠的性质可得:OD=AD=AB﹣BD=![]() ,
,
在Rt△OBD中,OD2=OB2+BD2,即(![]() )2=(2a)2+(
)2=(2a)2+(![]() b)2①,
b)2①,
在Rt△OAB中,OA2=OB2+AB2,即42=(2a)2+(2b)2②,
联立①②解得:![]() ,∴k=ab=
,∴k=ab=![]() .
.
故答案为:(1)(![]() ,0);(2)
,0);(2)![]() .
.

练习册系列答案
相关题目