Question

【题目】光明中学为了解学生对食堂工作的满意程度，8年级2班数学兴趣小组在全校甲、乙两个班内进行了调查统计，将调查结果分为不满意、一般、满意、非常满意四类，回收、整理好全部问卷后，得到下列不完整的统计图.

请结合图中信息，解决下列问题：

（1）求此次调查中接受调查的人数；

（2）求此次调查中结果为非常满意的人数；

（3）兴趣小组准备从调查结果为一般的4位同学中随机选择2位进行回访，已知4位同学中有2位来自甲班，另2位来自乙班，请用列表或用画树状图的方法求出选择的同学均来自甲班的概率.

Answer 1

【答案】（1）25人；（2）9人；（3）

【解析】

（1）由满意的有10人，占40%，即可求得此次调查中接受调查的人数．

（2）由总人数×非常满意的人数所占的百分比，即可求得此次调查中结果为非常满意的人数．

（3）首先根据题意画出树状图，然后由树状图求得所有等可能的结果与选择的同学均来自甲班的情况，再利用概率公式即可求得答案．

（1）∵满意的有10人，占40%，∴此次调查中接受调查的人数：10÷40%=25（人）；

（2）此次调查中结果为非常满意的人数为：25×36%=9（人）；

（3）画树状图得：

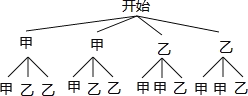
∵共有12种等可能的结果，选择的同学均来自甲班的有2种情况，∴选择的同学均来自甲班的概率为：．