题目内容
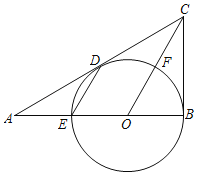
【题目】如图,抛物线y=﹣x2+bx+c经过A(0,3),C(2,n)两点,直线l:y=![]() x+2过C点,且与y轴交于点B,抛物线上有一动点E,过点E作直线EF⊥x轴于点F,交直线BC于点D
x+2过C点,且与y轴交于点B,抛物线上有一动点E,过点E作直线EF⊥x轴于点F,交直线BC于点D
(1)求抛物线的解析式.
(2)如图1,当点E在直线BC上方的抛物线上运动时,连接BE,BF,是否存在点E使直线BC将△BEF的面积分为2:3两部分?若存在,求出点E的坐标,若不存在说明理由;
(3)如图2,若点E在y轴右侧的抛物线上运动,连接AE,当∠AED=∠ABC时,直接写出此时点E的坐标.

【答案】(1)y=﹣x2+2x+3;(2)存在,E(![]() ,
,![]() )或(
)或(![]() ,
,![]() );(3)点E(
);(3)点E(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
【解析】
(1)直线l:y=![]() x+2过C点,则点C(2,3),y=
x+2过C点,则点C(2,3),y=![]() x+2过C点,且与y轴交于点B,则点B(0,2),即可求解;(2)
x+2过C点,且与y轴交于点B,则点B(0,2),即可求解;(2)![]() =
=![]() =
=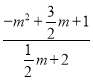 =
=![]() 或
或![]() ,即可求解;(3)分当点E在直线BC上方、点E在直线BC的下方两种情况,分别求解即可.
,即可求解;(3)分当点E在直线BC上方、点E在直线BC的下方两种情况,分别求解即可.
(1)直线l:y=![]() x+2过点C(2,n),且与y轴交于点B,
x+2过点C(2,n),且与y轴交于点B,
∴n=![]() ×2+2=3,当x=0时,y=2,
×2+2=3,当x=0时,y=2,
∴B(0,2),C(2,3)
将点A、C的坐标代入二次函数表达式得:![]() ,
,
解得:![]() ,
,
∴抛物线的表达式为:y=﹣x2+2x+3;
(2)设点E(m,﹣m2+2m+3),则点D(m,![]() m+2),
m+2),
∴DE=﹣m2+![]() m+1,DF=
m+1,DF=![]() m+2,
m+2,
![]() =
=![]() =
=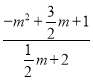 =
=![]() 或
或![]() ,
,
解得:m=![]() 或
或![]() ,
,
∴﹣m2+2m+3=![]() ,或﹣m2+2m+3=
,或﹣m2+2m+3=![]() ,
,
∴点E(![]() ,
,![]() )或(
)或(![]() ,
,![]() );
);
(3)由(2)知:E(m,﹣m2+2m+3),则点D(m,![]() m+2),
m+2),
DE=﹣m2+![]() m+1,DF=
m+1,DF=![]() m+2,
m+2,
①如图2,当点E在直线BC上方时,
∵AB∥EF,∠ABD+∠EDB=180°,
∵∠AED=∠ABC,
∴∠AED+∠EDB=180°,
∴AE∥CD,
∴四边形ABDE为平行四边形,
∴AB=DE=1=﹣m2+![]() m+1,
m+1,
解得:m=0或![]() (舍去0);
(舍去0);
∴﹣m2+2m+3=![]() ,即E(
,即E(![]() ,
,![]() ).
).
②如图3,当点E在直线BC的下方时,
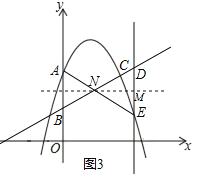
设AE、BD交于点N,过点N作x轴的平行线交DE于点M
∵AB∥DE,
∴∠ABN=∠NDE,而∠AED=∠ABC,
∴∠ABN=∠NDE=∠AED=∠ABC,
∴△NAB、△DEN都是以点N为顶点的等腰三角形,
∴点M的纵坐标和AB中点的坐标同为![]() ,
,
由中点公式得:![]() (﹣m2+2m+3+
(﹣m2+2m+3+![]() m+2)=
m+2)=![]() ,
,
解得:m=0或![]() (舍去0),
(舍去0),
∴﹣m2+2m+3=![]() ,即E(
,即E(![]() ,
,![]() ).
).
综上,点E(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).

 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案