Question

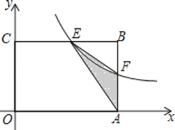
【题目】如图，已知直线与轴交于点A，与y轴交于点C，矩形ACBE的顶点B在第一象限的反比例函数图像上，过点B作，垂足为F，设OF=t．

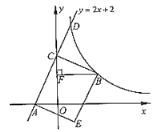
（1）求∠ACO的正切值；

（2）求点B的坐标（用含t的式子表示）；

（3）已知直线与反比例函数图像都经过第一象限的点D，联结DE，如果轴，求m的值．

Answer 1

【答案】（1）∠ACO的正切值为；（2）点B的坐标；（3）m的值为．

【解析】

（1）根据一次函数解析式算出点的坐标即可求算；

（2）根据矩形的性质得出，从而表示的坐标；

（3）作轴，根据矩形的性质得出，从而表示出的坐标，再根据条件表示的坐标，再根据均在反比例图象上从而算出

（1）∵直线与轴交于点A，与轴交于点C

∴

∴

（2）∵四边形是矩形，，

∴

∴

∴即

∴

∴

∴点B的坐标

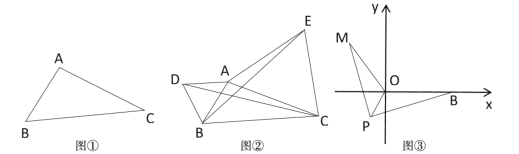
（3）

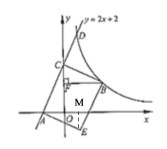
如图;作轴

∵四边形是矩形

∴

∴

∴

∴

∴点的横坐标为

又∵轴，在上

∴

∵,均在反比例上：

∴

解得：

∵四边形是矩形

∴舍去

∴

∴