题目内容
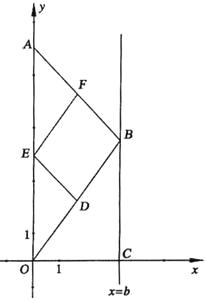
【题目】(1)发现:如图①,点A为一动点,点B和点C为两个定点,且![]() ,
,![]() (
(![]() ).
).
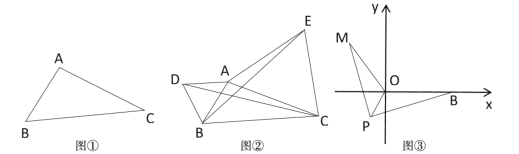
填空:当点![]() 位于_______时,线段
位于_______时,线段![]() 的长取得最小值,且最小值为_______(用含
的长取得最小值,且最小值为_______(用含![]() 的式子表示);
的式子表示);
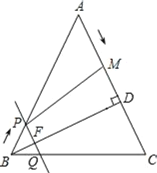
(2)如图②应用:点![]() 为线段
为线段![]() 外一动点,且
外一动点,且![]() ,
,![]() ,如图2分别以
,如图2分别以![]() 、
、![]() 为边作等边三角形
为边作等边三角形![]() 和等边三角形
和等边三角形![]() ,连接
,连接![]() 、
、![]() .
.
①请找出图中与![]() 相等的线段,并说明理由;
相等的线段,并说明理由;
②直接写出线段![]() 长的最小值.
长的最小值.
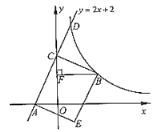
(3)拓展:如图3,在平面直角坐标系中,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 为线段OB外一动点,且
为线段OB外一动点,且![]() ,
,![]() ,
,![]() ,请求出
,请求出![]() 的最小值并直接写出点
的最小值并直接写出点![]() 的坐标.
的坐标.
【答案】(1)线段BC上,![]() ;(2)①
;(2)①![]() ,理由见解析;②
,理由见解析;②![]() ;(3)
;(3)![]()
【解析】
(1)直接根据三角形三边关系即可得出答案;
(2)①首先根据等边三角形的性质得出![]() ,然后由全等三角形的性质即可得出答案;
,然后由全等三角形的性质即可得出答案;
②线段BE长度的最小值=线段CD长度的最小值,当点D在BC边上时,CD最小,即可求出答案;
(3)在y轴上取点![]() ,连接
,连接![]() ,在点P所在的圆O上取一点
,在点P所在的圆O上取一点![]() ,连接
,连接![]() ,依题意作
,依题意作![]() ,使
,使![]() ,连接
,连接![]() ,首先利用相似三角形的性质得出点M在以
,首先利用相似三角形的性质得出点M在以![]() 为圆心的圆上运动,
为圆心的圆上运动,![]() ,从而可求出OM的最小值,此时M在y轴上,通过全等三角形的性质得出
,从而可求出OM的最小值,此时M在y轴上,通过全等三角形的性质得出![]() ,然后设
,然后设![]() ,建立方程组即可求出此时P点的坐标.
,建立方程组即可求出此时P点的坐标.
(1)![]() ,
,![]() ,
,![]() ,
,
∴当点A位于线段BC上时,线段AC的长取得最小值,且最小值为![]() ;
;
(2)①![]() ,理由如下:
,理由如下:
∵![]() 都是等边三角形,
都是等边三角形,
∴![]() ,
,
![]() ,
,
即![]() .
.
在![]() 和
和![]() 中,
中,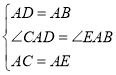
![]() ,
,
![]() ;
;
②当点D在BC边上时,CD最小,此时 ![]() ,
,
∵![]() ,
,
∴线段![]() 长的最小值为
长的最小值为![]() ;
;
(3)在y轴上取点![]() ,连接
,连接![]() ,在点P所在的圆O上取一点
,在点P所在的圆O上取一点![]() ,连接
,连接![]() ,依题意作
,依题意作![]() ,使
,使![]() ,连接
,连接![]() ,
,
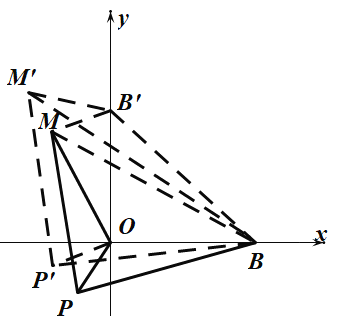
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
∴![]() ,
,
![]() ,
,
![]() .
.
同理,![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
∴点M在以![]() 为圆心的圆上运动,
为圆心的圆上运动,![]() ,
,
∴OM的最小值为![]() .
.
如图,此时M点在y轴上,设此时P点为![]() ,过点
,过点![]() 作
作![]() 轴于点E,延长
轴于点E,延长![]() ,过点B作
,过点B作![]() 于点F,
于点F,

∵![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
在![]() 和
和![]() 中,
中,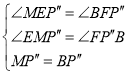
![]() ,
,
![]() .
.
设![]() ,
,
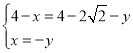 解得
解得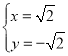
∴此时P的坐标为![]() .
.

 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案