题目内容
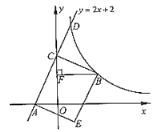
【题目】如图,在矩形OABC中,OA=3,OC=2,F是AB上的一个动点(F不与A,B重合),过点F的反比例函数y=![]() (x>0)的图象与BC边交于点E.
(x>0)的图象与BC边交于点E.
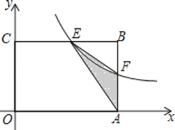
(1)当F为AB的中点时,求该反比例函数的解析式和点E的坐标.
(2)设过(1)中的直线EF的解析式为y=ax+b,直接写出不等式ax+b<![]() 的解集.
的解集.
(3)当k为何值时,△AEF的面积最大,最大面积是多少?
【答案】(1)y=![]() ,E点坐标为(
,E点坐标为(![]() ,2);(2)0<x<
,2);(2)0<x<![]() 或x>3;(3)当k的值为3时,△AEF的面积最大,最大面积为
或x>3;(3)当k的值为3时,△AEF的面积最大,最大面积为![]() .
.
【解析】
(1)由条件可求得F点坐标为(3,1),代入函数解析式可求得k,可求得反比例函数解析式,再令y=2代入可求得x的值,可求得E点坐标;
(2)由(1)的条件中E、F的坐标,结合函数图象可求得答案;
(3)可用k分别表示出点E、F的坐标,从而可表示出△AEF的面积,再利用二次函数的性质可求得其最大值.
(1)∵四边形OABC为矩形,OA=3,OC=2,
∴AB=2,BC=3,
∵F为AB的中点,
∴点F坐标为(3,1),
∵点F在反比例函数y=![]() (x>0)的图象上,
(x>0)的图象上,
∴k=3×1=3,
∴反比例函数解析式为y=![]() ,
,
∵点E在BC上,
∴E点纵坐标为2,
在y=![]() 中,令y=2,可求x=
中,令y=2,可求x=![]() ,
,
∴E点坐标为(![]() ,2);
,2);
(2)不等式ax+b<![]() 的解集即直线在反比例函数下方时对应的自变量的取值范围,
的解集即直线在反比例函数下方时对应的自变量的取值范围,
由(1)可知点E、F两点的横坐标分别为![]() 、3,
、3,
∴不等式ax+b<![]() 的解集为:0<x<
的解集为:0<x<![]() 或x>3;
或x>3;
(3)由题意可知点E的纵坐标为为2,点F的横坐标为3,且E、F在反比例函数y=![]() (x>0)的图象上,
(x>0)的图象上,
∴可设E(![]() ,2),F(3,
,2),F(3,![]() ),
),
∴AF=![]() ,CE=
,CE=![]() ,
,
∴BE=BC﹣CE=3﹣![]() ,
,
∴S△AEF=![]() AFBE=
AFBE=![]()
![]() (3﹣
(3﹣![]() )=﹣
)=﹣![]() k2+
k2+![]() =﹣
=﹣![]() (k﹣3)2+
(k﹣3)2+![]() ,
,
∵﹣![]() <0,
<0,
∴S△AEF是关于k的开口向下的抛物线,
∴当k=3时,S△AEF有最大值,最大值为![]() ,
,
即当k的值为3时,△AEF的面积最大,最大面积为![]() .
.