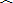题目内容
如图,⊙O是△ABC的外接圆,AO⊥BC于F,D为
的中点,E是BA延长线上一点,∠DAE=126°,则∠CAD等于( )

 |
| AC |
| A.36° | B.42° | C.38° | D.27° |

∵AO⊥BC,且AO是⊙O的半径,
∴AO垂直平分BC,
∴AB=AC,即∠ABC=∠ACB,
∵D是
的中点,
∴∠ABC=2∠DCA=2∠DAC,
∴∠ACB=2∠DCA,
∵四边形ABCD内接于⊙O,
∴∠BCD=∠DAE=126°,
∴∠ACB+∠DCA=126°,
即3∠DCA=126°,
∴∠DAC=∠DCA=42°.
故选B.
∴AO垂直平分BC,
∴AB=AC,即∠ABC=∠ACB,
∵D是
 |
| AC |
∴∠ABC=2∠DCA=2∠DAC,
∴∠ACB=2∠DCA,
∵四边形ABCD内接于⊙O,
∴∠BCD=∠DAE=126°,
∴∠ACB+∠DCA=126°,
即3∠DCA=126°,
∴∠DAC=∠DCA=42°.
故选B.

练习册系列答案
相关题目