题目内容
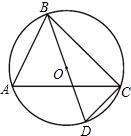
已知四边形ABCD内接于圆0，且AD∥BC，试判定四边形ABCD的形状，并说明理由．
（1）若AB∥CD，则ABCD为矩形．如图：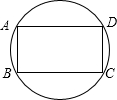
∵AD∥BC，AB∥CD，
∴四边形ABCD为平行四边形，
∴∠B=∠D，
∵圆内接四边形对角互补，
∴∠B+∠D=180°，
∴∠B=∠D=90°，
∴?ABCD为矩形．
（2）若AB不平行于CD，则ABCD为等腰梯形．如图：
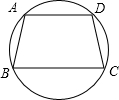∵AB=CD，而AB不平行于CD，
又∵AD∥BC，
∴
=
，
∴AB=CD，
∴ABCD是等腰梯形．
∵AD∥BC，AB∥CD，
∴四边形ABCD为平行四边形，
∴∠B=∠D，
∵圆内接四边形对角互补，
∴∠B+∠D=180°，
∴∠B=∠D=90°，
∴?ABCD为矩形．
（2）若AB不平行于CD，则ABCD为等腰梯形．如图：
∵AB=CD，而AB不平行于CD，又∵AD∥BC，
∴
 |
| AB |
|
| CD |
∴AB=CD，
∴ABCD是等腰梯形．
练习册系列答案
相关题目
