题目内容
【题目】综合与探究
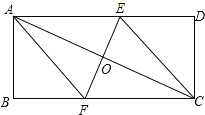
如图,抛物线y=﹣![]() x2﹣
x2﹣![]() x+
x+![]() 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,直线l经过B、C两点,点M从点A出发以每秒1个单位长度的速度向终点B运动,连接CM,将线段MC绕点M顺时针旋转90°得到线段MD,连接CD、BD.设点M运动的时间为t(t>0),请解答下列问题:
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,直线l经过B、C两点,点M从点A出发以每秒1个单位长度的速度向终点B运动,连接CM,将线段MC绕点M顺时针旋转90°得到线段MD,连接CD、BD.设点M运动的时间为t(t>0),请解答下列问题:

(1)求点A的坐标与直线l的表达式;
(2)①请直接写出点D的坐标(用含t的式子表示),并求点D落在直线l上时t的值;
②求点M运动的过程中线段CD长度的最小值.
【答案】(1)A(﹣3,0),y=﹣![]() x+
x+![]() ;(2)①点D落在直线l上时,t=6﹣2
;(2)①点D落在直线l上时,t=6﹣2![]() ;②CD的最小值为
;②CD的最小值为![]() .
.
【解析】
(1)解方程求出点A、点B的坐标,根据二次函数的性质求出点C的坐标,利用待定系数法求出直线l的表达式;
(2)①分点M在AO上运动、点M在OB上运动两种情况,DN⊥x轴于N,证明△MCO≌△DMN,根据全等三角形的性质得到MN=OC=![]() ,DN=OM=3﹣t,得到点D的坐标,根据一次函数图象上点的坐标特征求出t;
,DN=OM=3﹣t,得到点D的坐标,根据一次函数图象上点的坐标特征求出t;
②根据等腰直角三角形的性质、垂线段最短解答.
(1)当y=0时,﹣![]() x2﹣
x2﹣![]() x+
x+![]() =0,
=0,
解得x1=1,x2=﹣3,
∵点A在点B的左侧,
∴A(﹣3,0),B(1,0),
当x=0时,y=![]() ,即C(0,
,即C(0,![]() ),
),
设直线l的表达式为y=kx+b,
将B,C两点坐标代入得,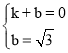 ,
,
解得,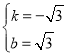 ,
,
则直线l的表达式为y=﹣![]() x+
x+![]() ;
;
(2)①如图1,当点M在AO上运动时,过点D作DN⊥x轴于N,
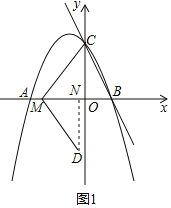
由题意可知,AM=t,OM=3﹣t,MC⊥MD,
则∠DMN+∠CMO=90°,∠CMO+∠MCO=90°,
∴∠MCO=∠DMN,
在△MCO与△DMN中,
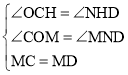 ,
,
∴△MCO≌△DMN(AAS),
∴MN=OC=![]() ,DN=OM=3﹣t,
,DN=OM=3﹣t,
∴D(t﹣3+![]() ,t﹣3);
,t﹣3);
同理,如图2,当点M在OB上运动时,
点D的坐标为:D(﹣3+t+![]() ,t﹣3)
,t﹣3)
将D点坐标代入直线BC的解析式y=﹣![]() x+
x+![]() 得,t﹣3=﹣
得,t﹣3=﹣![]() ×(﹣3+t+
×(﹣3+t+![]() )+
)+![]() ,
,
t=6﹣2![]() ,即点D落在直线l上时,t=6﹣2
,即点D落在直线l上时,t=6﹣2![]() ;
;
②∵△COD是等腰直角三角形,
∴CM=MD,
∴线段CM最小时,线段CD长度的最小,
∵M在AB上运动,
∴当CM⊥AB时,CM最短,CD最短,即CM=CO=![]() ,
,
根据勾股定理得,CD的最小值为![]() .
.
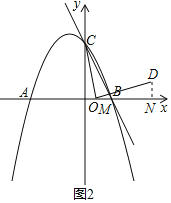

 阅读快车系列答案
阅读快车系列答案【题目】二次函数![]() (
(![]() 是常数,
是常数,![]() )的自变量
)的自变量![]() 与函数值
与函数值![]() 的部分对应值如下表:
的部分对应值如下表:
| … |
|
| 0 | 1 | 2 | … |
| … |
|
|
|
|
| … |
且当![]() 时,与其对应的函数值
时,与其对应的函数值![]() .有下列结论:①
.有下列结论:①![]() ;②
;②![]() 和3是关于
和3是关于![]() 的方程
的方程![]() 的两个根;③
的两个根;③![]()
![]() .其中,正确结论的个数是( )
.其中,正确结论的个数是( )
A. 0B. 1C. 2D. 3