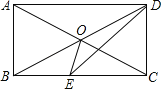
题目内容
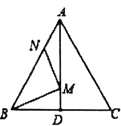
【题目】如图,四边形ABCD是菱形,∠A=60°,AB=2,扇形EBF的半径为2,圆心角为60°,则图中阴影部分的面积是_____.
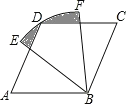
【答案】![]()
【解析】
连接BD,易证△DAB是等边三角形,即可求得△ABD的高为![]() ,再证明△ABG≌△DBH,即可得四边形GBHD的面积等于△ABD的面积,由图中阴影部分的面积为S扇形EBF﹣S△ABD即可求解.
,再证明△ABG≌△DBH,即可得四边形GBHD的面积等于△ABD的面积,由图中阴影部分的面积为S扇形EBF﹣S△ABD即可求解.
如图,连接BD.
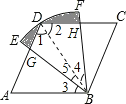
∵四边形ABCD是菱形,∠A=60°,
∴∠ADC=120°,
∴∠1=∠2=60°,
∴△DAB是等边三角形,
∵AB=2,
∴△ABD的高为![]() ,
,
∵扇形BEF的半径为2,圆心角为60°,
∴∠4+∠5=60°,∠3+∠5=60°,
∴∠3=∠4,
设AD、BE相交于点G,设BF、DC相交于点H,
在△ABG和△DBH中,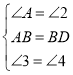 ,
,
∴△ABG≌△DBH(ASA),
∴四边形GBHD的面积等于△ABD的面积,
∴图中阴影部分的面积是:S扇形EBF﹣S△ABD=![]() ﹣
﹣![]() ×2×
×2×![]() =
=![]() .
.
故答案是:![]() .
.

【题目】为了调查学生对垃圾分类及投放知识的了解情况,从甲、乙两校各随机抽取40名学生进行了相关知识测试,获得了他们的成绩(百分制),并对数据(成绩)进行了整理、描述和分析.下面给出了部分信息.
a.甲、乙两校40名学生成绩的频数分布统计表如下:
成绩x 学校 |
|
|
|
|
|
甲 | 4 | 11 | 13 | 10 | 2 |
乙 | 6 | 3 | 15 | 14 | 2 |
(说明:成绩80分及以上为优秀,70~79分为良好,60~69分为合格,60分以下为不合格)
b.甲校成绩在![]() 这一组的是:
这一组的是:
70 70 70 71 72 73 73 73 74 75 76 77 78
c.甲、乙两校成绩的平均分、中位数、众数如下:
学校 | 平均分 | 中位数 | 众数 |
甲 | 74.2 | n | 85 |
乙 | 73.5 | 76 | 84 |
根据以上信息,回答下列问题:
(1)写出表中n的值;
(2)在此次测试中,某学生的成绩是74分,在他所属学校排在前20名,由表中数据可知该学生是_____________校的学生(填“甲”或“乙”),理由是__________;
(3)假设乙校800名学生都参加此次测试,估计成绩优秀的学生人数.
【题目】某家具商场计划购进某种餐桌、餐椅进行销售,有关信息如表:
原进价(元/张) | 零售价(元/张) | 成套售价(元/套) | |
餐桌 | a | 270 | 500元 |
餐椅 | a﹣110 | 70 |
已知用600元购进的餐桌数量与用160元购进的餐椅数量相同.
(1)求表中a的值;
(2)若该商场购进餐椅的数量是餐桌数量的5倍还多20张,且餐桌和餐椅的总数量不超过200张.该商场计划将一半的餐桌成套(一张餐桌和四张餐椅配成一套)销售,其余餐桌、餐椅以零售方式销售.请问怎样进货,才能获得最大利润?最大利润是多少?
(3)由于原材料价格上涨,每张餐桌和餐椅的进价都上涨了10元,但销售价格保持不变.商场购进了餐桌和餐椅共200张,应怎样安排成套销售的销售量(至少10套以上),使得实际全部售出后,最大利润与(2)中相同?请求出进货方案和销售方案.
【题目】受国内外复杂多变的经济环境影响,去年1至7月,原材料价格一路攀升,长沙市某服装厂每件衣服原材料的成本y1(元)与月份x(1≤x≤7,且x为整数)之间的函数关系如下表:
月份x | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
成本(元/件) | 56 | 58 | 60 | 62 | 64 | 66 | 68 |
8至12月,随着经济环境的好转,原材料价格的涨势趋缓,每件原材料成本y2(元)与月份x的函数关系式为y2=x+62(8≤x≤12,且x为整数).
(1)请观察表格中的数据,用学过的函数相关知识求y1与x的函数关系式.
(2)若去年该衣服每件的出厂价为100元,生产每件衣服的其他成本为8元,该衣服在1至7月的销售量p1(万件)与月份x满足关系式p1=0.1x+1.1(1≤x≤7,且x为整数); 8至12月的销售量p2(万件)与月份x满足关系式p2=﹣0.1x+3(8≤x≤12,且x为整数),该厂去年哪个月利润最大;并求出最大利润.