Question

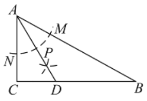
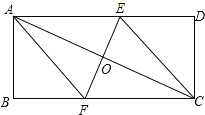
【题目】如图，矩形ABCD的对角线AC的垂直平分线EF与AD、AC、BC分别交于点E、O、F．

（1）求证：四边形AFCE是菱形；

（2）若AB＝5，BC＝12，求菱形AFCE的面积．

Answer 1

【答案】（1）详见解析；（2）

【解析】

（1）根据ABCD为矩形，根据矩形的对边平行得到AE与CF平行，由两直线平行得到一对内错角相等，又EF垂直平分AC，根据垂直平分线的定义得到AO=CO，且AC与EF垂直，再加上一对对顶角相等，利用“ASA”得到三角形AOE与三角形COF全等，根据全等三角形的对应边相等得到AE=FC，由一组对边平行且相等的四边形为平行四边形得到AFCE为平行四边形，又根据对角线垂直的平行四边形为菱形即可得证；

（2）由矩形的性质得到∠B为直角，在直角三角形ABC中，由AB与BC的长，利用勾股定理求出AC的长，又已知EF的长，而AC与EF为菱形AFCE的两条对角线，根据对角线乘积的一半即可求出菱形的面积．

解：（1）∵四边形ABCD是矩形，

∴AE∥FC，

∴∠EAO＝∠FCO，

∵EF垂直平分AC，

∴AO＝CO，FE⊥AC，

又∠AOE＝∠COF，

∴△AOE≌△COF（AAS），

∴EO＝FO，

∴四边形AFCE为平行四边形，

又∵FE⊥AC，

∴平行四边形AFCE为菱形；

（2）如图，在Rt△ABC中，由AB＝5，BC＝12，

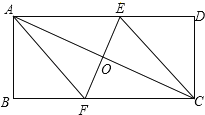
根据勾股定理得：AC＝＝13，

∴OA＝，

∵∠EAO＝∠ACB，

∴tan∠EAO＝tan∠ACB，

∴，即，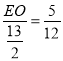

∴EO＝，

∴EF＝，

∴菱形AFCE的面积S＝ACEF＝；