Question

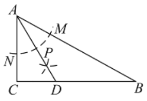
【题目】如图，在△ABD中，∠ABD = ∠ADB，分别以点B，D为圆心，AB长为半径在BD的右侧作弧，两弧交于点C，连接BC，DC和AC，AC与BD交于点O．

（1）用尺规补全图形，并证明四边形ABCD为菱形；

（2）如果AB = 5，，求BD的长．

Answer 1

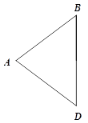
【答案】（1）补全的图形如图所示．证明见解析；（2）BD=6.

【解析】

（1）根据作法画出对应的几何图形得到四边形ABCD；先利用∠ABD=∠ADB得到AB=AD．再利用作法得到BC=DC=AD=AB，从而可判断四边形ABCD为菱形；

（2）利用菱形的性质得到BD⊥AC，OB=OD，则根据计算出BO，从而得到BD的长．

（1）补全的图形如图所示．

证明：由题意可知BC = DC = AB，

∵ 在△ABD中，，

∴ AB = AD，

∴ BC = DC = AD = AB，

∴ 四边形ABCD为菱形；

（2）∵ 四边形ABCD为菱形，

∴ BD⊥AC，OB=OD，

在Rt△ABO中，，AB=5，，

∴ ，

∴ ．