题目内容
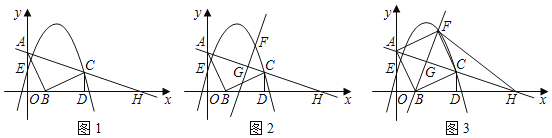
【题目】二次函数y = ![]() ax2 ax + c图象的顶点为C,一次函数y = x + 3的图象与这个二次函数的图象交于A、B两点(其中点A在点B的左侧),与它的对称轴交于点D.
ax2 ax + c图象的顶点为C,一次函数y = x + 3的图象与这个二次函数的图象交于A、B两点(其中点A在点B的左侧),与它的对称轴交于点D.
(1)求点D的坐标;
(2) ①若点C与点D关于x轴对称,且△BCD的面积等于4,求此二次函数的关系式;
②若CD=DB,且△BCD的面积等于4![]() ,求a的值.
,求a的值.
【答案】(1)点D的坐标为(1,2);(2)①![]() ;②
;②![]() 或
或 ![]()
【解析】
(1)函数的对称轴为:![]() ,当x=1时,y=-x+3=2,故点D(1,2);
,当x=1时,y=-x+3=2,故点D(1,2);
(2)①△BCD的面积=![]() ,求出B点坐标为(3,0),把B点坐标代入
,求出B点坐标为(3,0),把B点坐标代入![]() 即可求解;②设B(m,-m+3)(m>1),过点B作BE⊥CD于E,则BE=m﹣1,根据S△BCD=4
即可求解;②设B(m,-m+3)(m>1),过点B作BE⊥CD于E,则BE=m﹣1,根据S△BCD=4![]() , 得B(2
, 得B(2![]() +1,-2
+1,-2![]() +2),分两种情况:当a>0时,则点C在点D下方,当a<0时,则点C在点D上方,分别求解即可.
+2),分两种情况:当a>0时,则点C在点D下方,当a<0时,则点C在点D上方,分别求解即可.
(1)∵二次函数![]() 的对称轴为直线x=1,
的对称轴为直线x=1,
∴把x=1代入![]() ,得y=2,∴点D的坐标为(1,2).
,得y=2,∴点D的坐标为(1,2).
(2)∵点C与点D关于x轴对称,
∴点C的坐标为(1,-2),
∴CD=4.
①设点B横坐标为x,则![]() ,解得x=3.
,解得x=3.
∵B点在函数y=-x+3的图像上,
∴B点坐标为(3,0).
∵二次函数的顶点为C(1,-2),
∴它的函数关系式可设为![]() ,把B点坐标代入,得a=1,
,把B点坐标代入,得a=1,
∴此二次函数的关系式为![]() .
.
②设B(m,-m+3)(m>1),由y=-x+3可知y=-x+3图像与DC相交成45°,过点B作BE⊥CD于E,则BE=m﹣1,DB=DC=![]() BE,
BE,
由S△BCD=4![]() , 得
, 得![]() ×
×![]() (m﹣1)2=4
(m﹣1)2=4![]() ,
,
m =2![]() +1,m =-2
+1,m =-2![]() +1(舍去),
+1(舍去),
DC=4,B(2![]() +1,-2
+1,-2![]() +2),
+2),
当a>0时,则点C在点D下方,则点C的坐标为(1,-2),
B点代入![]() 得a=
得a=![]() ,
,
当a<0时,则点C在点D上方,则点C的坐标为(1,6),
B点代入![]() 得a=
得a=![]() ,
,
综上所述a的值为:![]() 或
或 ![]() .
.

 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案【题目】为了增强学生对新冠病毒预防知识的了解,我校初一年级开展了网上预防知识的宣传教育活动.为了解这次宣传教育活动的效果,学校从初一年级1500名学生中随机抽取部分学生进行网上知识测试(测试满分100分,得分均为整数),并根据抽取的学生测试成绩,制作了如下统计图表:
抽取学生知识测试成绩的频数表 | ||
成绩 | 频数(人) | 频率 |
| 10 | 0.1 |
| 15 |
|
|
| 0.2 |
| 40 |
|
|
|
|
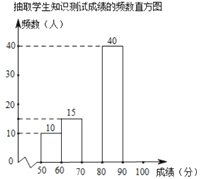
由图表中给出的信息回答下列问题:
(1)![]() ,
,![]() ,并补全频数直方图;
,并补全频数直方图;
(2)如果80分以上(包括80分)为优秀,请估计初一年级1500名学生中成绩优秀的人数;
(3)小强在这次测试中成绩为85分,你认为85分一定是这100名学生知识测试成绩的中位数吗?请简要说明理由.