题目内容
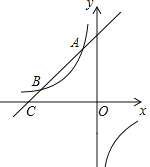
【题目】在平面直角坐标系xOy中,直线L:y=kx+2k(k>0)与x轴交于点A,与y轴交于点B,与函数![]() (x>0)的图象的交点P位于第一象限.
(x>0)的图象的交点P位于第一象限.
(1)若点P的坐标为(1,6),
①求m的值及点A的坐标;
②![]() =_________;
=_________;
(2)直线h:y=2kx-2与y轴交于点C,与直线L1交于点Q,若点P的横坐标为1,
①写出点P的坐标(用含k的式子表示);
②当PQ≤PA时,求m的取值范围.
【答案】(1)①6;(2,0)②![]() ;(2)①P(1,3k)②m≥3
;(2)①P(1,3k)②m≥3
【解析】
(1)①把P(1,6)代入函数![]() (x>0)即可求得m的值,直线l1:y=kx+2k(k>0)中,令y=0,即可求得x的值,从而求得A的坐标;
(x>0)即可求得m的值,直线l1:y=kx+2k(k>0)中,令y=0,即可求得x的值,从而求得A的坐标;
②把P的坐标代入y=kx+2k即可求得k的值,进而求得B的坐标,然后根据勾股定理求得PB和PA,即可求得![]() 的值;
的值;
(2)①把x=1代入y=kx+2k,求得y=3k,即可求得P(1,3k);
②分别过点P、Q作PM⊥x轴于M,QN⊥x轴于N,则点M、点N的横坐标1,2+![]() ,若PQ=PA,则
,若PQ=PA,则![]() =1,根据平行线分线段成比例定理则
=1,根据平行线分线段成比例定理则![]() =
=![]() =1,得出MN=MA=3,即可得到2+
=1,得出MN=MA=3,即可得到2+![]() 1=3,解得k=1,根据题意即可得到当
1=3,解得k=1,根据题意即可得到当![]() =
=![]() ≤1时,k≥1,则m=3k≥3.
≤1时,k≥1,则m=3k≥3.
(1)①令y=0,则kx+2k=0,
∵k>0,解得x=2,
∴点A的坐标为(2,0),
∵点P的坐标为(1,6),
∴m=1×6=6;
②∵直线l1:y=kx+2k(k>0)函数![]() (x>0)的图象的交点P,且P(1,6),
(x>0)的图象的交点P,且P(1,6),
∴6=k+2k,解得k=2,
∴y=2x+4,
令x=0,则y=4,
∴B(0,4),
∵点A的坐标为(2,0),
∴PA=![]() ,PB=
,PB=![]() ,
,
∴![]() =
=![]() ,
,
故答案为![]() ;
;
(2)①把x=1代入y=kx+2k得y=3k,
∴P(1,3k);
②由题意得,kx+2k=2kx2,
解得x=2+![]() ,
,
∴点Q的横坐标为2+![]() ,
,
∵2+![]() >1(k>0),
>1(k>0),
∴点Q在点P的右侧,
如图,分别过点P、Q作PM⊥x轴于M,QN⊥x轴于N,则点M、点N的横坐标为1,2+![]() ,
,
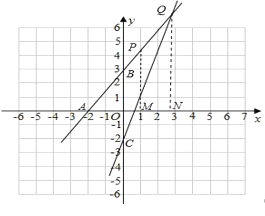
若PQ=PA,则![]() =1,
=1,
∴![]() =
=![]() =1,
=1,
∴MN=MA,
∴2+![]() 1=3,解得k=1,
1=3,解得k=1,
∵MA=3,
∴当![]() =
=![]() ≤1时,k≥1,
≤1时,k≥1,
∴m=3k≥3,
∴当PQ≤PA时,m≥3.

 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案