题目内容
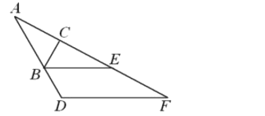
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=36°,△ABC的外角∠CBD的平分线BE交AC的延长线于点E.
(1)求∠CBE的度数;
(2)点F是AE延长线上一点,过点F作∠AFD=27°,交AB的延长线于点D.求证:BE∥DF.
【答案】(1)63°;(2)见解析
【解析】
(1)先根据直角三角形两锐角互余求出∠ABC=90°﹣∠A=54°,由邻补角定义得出∠CBD=126°.再根据角平分线定义即可求出∠CBE=63°;
(2)先根据三角形外角的性质得出∠CEB=90°﹣63°=27°,再根据∠F=27°,即可得出BE∥DF.
解:(1)∵在Rt△ABC中,∠ACB=90°,∠A=36°,
∴∠ABC=90°﹣∠A=54°,
∴∠CBD=126°.
∵BE是∠CBD的平分线,
∴∠CBE=![]() ∠CBD=63°;
∠CBD=63°;
(2)∵∠ACB=90°,∠CBE=63°,
∴∠CEB=90°﹣63°=27°.
又∵∠F=27°,
∴∠F=∠CEB=27°,
∴DF∥BE

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目






