Question

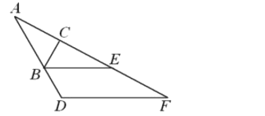
【题目】如图，在四边形ABCD中，∠B=90°，AD//BC，AD=16，BC=21，CD=13．

（1）求直线AD和BC之间的距离；

（2）动点P从点B出发，沿射线BC以每秒2个单位长度的速度运动，动点Q从点A出发，在线段AD上以每秒1个单位长度的速度运动，点P、Q同时出发，当点Q运动到点D时，两点同时停止运动，设运动时间为t秒．试求当t为何值时，以P、Q、D、C为顶点的四边形为平行四边形？

（3）在（2）的条件下，是否存在点P，使△PQD为等腰三角形？若存在，请直接写出相应的t值，若不存在，请说明理由．

Answer 1

【答案】（1）12；（2）5s或；（3）s或s或s

【解析】

（1）AD与BC之间的距离即AB的长，如下图，过点D作BC的垂线，交BC于点E，在RtDEC中可求得DE的长，即AB的长，即AD与BC间的距离；

（2）四边形QDCP为平行四边形，只需QD=CP即可；

（3）存在3大类情况，情况一：QP=PD，情况二：PD=QD，情况三：QP=QD，而每大类中，点P存在2种情况，一种为点P还未到达点C，另一种为点P从点C处返回．

（1）如下图，过点D作BC的垂线，交BC于点E

∵∠B=90°，AD∥BC

∴AB⊥BC，AB⊥AD

∴AB的长即为AD与BC之间的距离

∵AD=16，BC=21，

∴EC=5

∵DC=13

∴在RtDEC中，DE=12

同理，DE的长也是AD与BC之间的距离

∴AD与BC之间的距离为12

（2）∵AD∥BC

∴只需QD=PC，则四边形QDCP是平行四边形

QD=16－t，PC=21－2t或PC=2t－21

∴16－t=21－2t或16－t=2t－21

解得：t=5s或t=

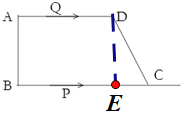
（3）情况一：QP=PD

图形如下，过点P作AD的垂线，交AD于点F

∵PQ=PD，PF⊥QD，

∴QF=FD

∵AF∥BP，AB∥FP，∠B=90°

∴四边形ABPF是矩形，

∴AF=BP

由题意得：AQ=t，则QD=16－t，QF=8－，AF=8+

BP=2t或BP=21－(2t－21)=42－2t

∵AF=BP

∴8+2t或8+42－2t

解得：t=或t=

情况二：PD=QD，图形如下，过点P作AD的垂线，交AD于点F

同理QD=16－t，PF=AB=12

BP=2t或21－(2t－21)=42－2t

则FD=AD－AF=AD－BP=16－2t或FD=16－(42－2t)=2t－26

∴在RtPFD中，或

∵PD=QD，

∴

∴或

解得：2个方程都无解

情况三：QP=QD，图形如下，过点P作AD的垂线，交AD于点F

同理：QD=16－t，FP=12

BP=2t或BP=42－2t

QF=AF－AQ=BP－AQ=2t－t=t或QF=42－2t－t=42－3t

在RtQFP中，或

∵PQ=QD，

∴

∴或

第一个方程解得：t=，第二个方程解得：无解

综上得：t=或或