题目内容
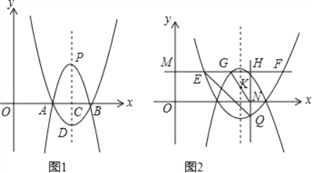
【题目】如图1,二次函数y1=(x﹣2)(x﹣4)的图象与x轴交于A、B两点(点A在点B的左侧),其对称轴l与x轴交于点C,它的顶点为点D.
(1)写出点D的坐标 .
(2)点P在对称轴l上,位于点C上方,且CP=2CD,以P为顶点的二次函数y2=ax2+bx+c(a≠0)的图象过点A.
①试说明二次函数y2=ax2+bx+c(a≠0)的图象过点B;
②点R在二次函数y1=(x﹣2)(x﹣4)的图象上,到x轴的距离为d,当点R的坐标为 时,二次函数y2=ax2+bx+c(a≠0)的图象上有且只有三个点到x轴的距离等于2d;
③如图2,已知0<m<2,过点M(0,m)作x轴的平行线,分别交二次函数y1=(x﹣2)(x﹣4)y2=ax2+bx+c(a≠0)的图象于点E、F、G、H(点E、G在对称轴l左侧),过点H作x轴的垂线,垂足为点N,交二次函数y1=(x﹣2)(x﹣4)的图象于点Q,若△GHN∽△EHQ,求实数m的值.

【答案】(1)(3,﹣1)(2)①二次函数y2=ax2+bx+c(a≠0)的图象过点B②(3﹣![]() ,1)、(3+
,1)、(3+![]() ,1)或(3,﹣1)③当△GHN∽△EHQ,实数m的值为1.
,1)或(3,﹣1)③当△GHN∽△EHQ,实数m的值为1.
【解析】(1)∵y1=(x﹣2)(x﹣4)=x2﹣6x+8=(x﹣3)2﹣1,
∴顶点D的坐标为(3,﹣1).故答案为:(3,﹣1).
(2)①∵点P在对称轴l上,位于点C上方,且CP=2CD,∴点P的坐标为(3,2),
∴二次函数y1=(x﹣2)(x﹣4)与y2=ax2+bx+c的图象的对称轴均为x=3,
∵点A、B关于直线x=3对称,∴二次函数y2=ax2+bx+c(a≠0)的图象过点B.
②∵二次函数y2=ax2+bx+c的顶点坐标P(3,2),且图象上有且只有三个点到x轴的距离等于2d,∴2d=2,解得:d=1.令y1=(x﹣2)(x﹣4)=x2﹣6x+8中y1=±1,即x2﹣6x+8=±1,
解得:x1=3﹣![]() ,x2=3+
,x2=3+![]() ,x3=3,∴点R的坐标为(3﹣
,x3=3,∴点R的坐标为(3﹣![]() ,1)、(3+
,1)、(3+![]() ,1)或(3,﹣1).
,1)或(3,﹣1).
故答案为:(3﹣![]() ,1)、(3+
,1)、(3+![]() ,1)或(3,﹣1).
,1)或(3,﹣1).
③设过点M平行x轴的直线交对称轴l于点K,直线l也是二次函数y2=ax2+bx+c(a≠0)的图象的对称轴.
∵二次函数y2=ax2+bx+c过点A、B,且顶点坐标为P(3,2),
∴二次函数y2=﹣2(x﹣2)(x﹣4).
设N(n,0),则H(n,﹣2(n﹣2)(n﹣4)),Q(n,(n﹣2)(n﹣4)),
∴HN=2(n﹣2)(n﹣4),QN=(n﹣2)(n﹣4),∴![]() =2,即
=2,即![]() =
=![]() .
.
∵△GHN∽△EHQ,∴![]() .∵G、H关于直线l对称,∴KG=KH=
.∵G、H关于直线l对称,∴KG=KH=![]() HG,∴
HG,∴![]() .
.
设KG=t(t>0),则G的坐标为(3﹣t,m),E的坐标为(3﹣2t,m),
由题意得:![]() ,解得:
,解得: 或
或![]() (舍去).
(舍去).
故当△GHN∽△EHQ,实数m的值为1.

 一本好题口算题卡系列答案
一本好题口算题卡系列答案【题目】(7分)某产品每件的成本10元,试销阶段每件产品的销售价![]() (元)与产品的日销售量
(元)与产品的日销售量![]() (件)之间的关系如下表:
(件)之间的关系如下表:
| 15 | 20 | 30 | … |
| 25 | 20 | 10 | … |
且日销售量![]() (件)是销售价
(件)是销售价![]() (元)的一次函数.
(元)的一次函数.
(1)求出日销售量![]() (件)与销售价
(件)与销售价![]() (元)的函数关系式;
(元)的函数关系式;
(2)要使每日的销售利润最大,每件产品的销售价应定为多少元?此时最大销售利润是多少?