题目内容
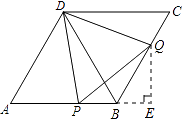
【题目】如图，在菱形ABCD中，∠A=60°，点P、Q分别在边AB、BC上，且AP=BQ． 
（1）求证：△BDQ≌△ADP；
（2）已知AD=3，AP=2，求cos∠BPQ的值（结果保留根号）．
【答案】
（1）证明：∵四边形ABCD是菱形，
∴AD=AB，∠ABD=∠CBD= 
∠ABC，AD∥BC，
∵∠A=60°，
∴△ABD是等边三角形，∠ABC=120°，
∴AD=BD，∠CBD=∠A=60°，
∵AP=BQ，
∴△BDQ≌△ADP（SAS）
（2）解：过点Q作QE⊥AB，交AB的延长线于E，
∵BQ=AP=2，
∵AD∥BC，
∴∠QBE=60°，
∴QE=QBsin60°=2× 
= 
，BE=QBcos60°=2× =1，
∵AB=AD=3，
∴PB=AB﹣AP=3﹣2=1，
∴PE=PB+BE=2，
∴在Rt△PQE中，PQ= 
= 
，
∴cos∠BPQ= 
= 
= 
．
【解析】（1）由四边形ABCD是菱形，可证得AD=AB，∠ABD=∠CBD= ∠ABC，AD∥BC，又由∠A=60°，易得△ABD是等边三角形，然后由SAS即可证得△BDQ≌△ADP；（2）首先过点Q作QE⊥AB，交AB的延长线于E，然后由三角函数的性质，即可求得PE与QE的长，又由勾股定理，即可求得PQ的长，则可求得cos∠BPQ的值．
【考点精析】关于本题考查的菱形的性质和解直角三角形，需要了解菱形的四条边都相等；菱形的对角线互相垂直，并且每一条对角线平分一组对角；菱形被两条对角线分成四个全等的直角三角形；菱形的面积等于两条对角线长的积的一半；解直角三角形的依据：①边的关系a2+b2=c2；②角的关系：A+B=90°；③边角关系：三角函数的定义．(注意：尽量避免使用中间数据和除法)才能得出正确答案．
