题目内容
【题目】已知,在矩形ABCD中,AB=4,BC=2,点M为边BC的中点,点P为边CD上的动点(点P异于C,D两点).连接PM,过点P作PM的垂线与射线DA相交于点E(如图),设CP=x,DE=y.
(1)写出y与x之间的关系式;
(2)若点E与点A重合,则x的值为;
(3)是否存在点P,使得点D关于直线PE的对称点D′落在边AB上?若存在,求x的值;若不存在,请说明理由. 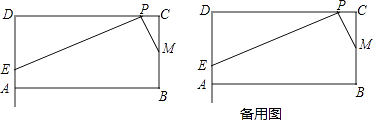
【答案】
(1)y=﹣x2+4x
(2)2+ ![]() 或2﹣
或2﹣ ![]()
(3)解:存在,过P作PH⊥AB于点H,

∵点D关于直线PE的对称点D′落在边AB上,
∴PD′=PD=4﹣x,ED′=ED=y=﹣x2+4x,EA=AD﹣ED=x2﹣4x+2,∠PD′E=∠D=90°,
在Rt△D′PH中,PH=2,D′P=DP=4﹣x,
根据勾股定理得:D′H= ![]() =
= ![]() ,
,
∵∠ED′A=180°﹣90°﹣∠PD′H=90°﹣∠PD′H=∠D′PH,∠PD′E=∠PHD′=90°,
∴△ED′A∽△D′PH,
∴ ![]() ,即
,即 ![]() =
= ![]() =x=
=x= ![]() ,
,
整理得:2x2﹣4x+1=0,
解得:x= ![]() .
.
当x= ![]() 时,y=﹣(
时,y=﹣( ![]() )2+4×
)2+4× ![]() =
= ![]() >2,
>2,
此时,点E在边DA的延长线上,D关于直线PE的对称点不可能落在边AB上,所以舍去.
当x= ![]() 时,y=﹣(
时,y=﹣( ![]() )2+4×
)2+4× ![]() =
= ![]() <2,此时,点E在边AD上,符合题意.
<2,此时,点E在边AD上,符合题意.
所以当x= ![]() 时,点D关于直线PE的对称点D′落在边AB上
时,点D关于直线PE的对称点D′落在边AB上
【解析】解:(1)∵PE⊥PM,∴∠EPM=90°, ∴∠DPE+∠CPM=90°,
又矩形ABCD,∴∠D=90°,
∴∠DPE+∠DEP=90°,
∴∠CPM=∠DEP,又∠C=∠D=90°,
∴△CPM∽△DEP,
∴ ![]() ,
,
又CP=x,DE=y,AB=DC=4,∴DP=4﹣x,
又M为BC中点,BC=2,∴CM=1,
∴ ![]() ,
,
则y=﹣x2+4x;
所以答案是:y=﹣x2+4x;(2)当E与A重合时,DE=AD=2,
∵△CPM∽△DEP,
∴ ![]() ,
,
又CP=x,DE=2,CM=1,DP=4﹣x,
∴ ![]() ,即x2﹣4x+2=0,
,即x2﹣4x+2=0,
解得:x=2+ ![]() 或x=2﹣
或x=2﹣ ![]() ,
,
则x的值为2+ ![]() 或2﹣
或2﹣ ![]() ;
;
所以答案是:2+ ![]() 或2﹣
或2﹣ ![]() ;
;
【考点精析】解答此题的关键在于理解矩形的性质的相关知识,掌握矩形的四个角都是直角,矩形的对角线相等,以及对翻折变换(折叠问题)的理解,了解折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等.

 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案【题目】今年我市体育中考的现场选测项目中有一项是“排球30秒对墙垫球”,为了了解某学校九年级学生此项目平时的训练情况,随机抽取了该校部分九年级学生进行测试,根据测试结果,制作了如下尚不完整的频数分布表:
组别 | 垫球个数x(个) | 频数(人数) | 频率 |
1 | 10≤x<20 | 5 | 0.10 |
2 | 20≤x<30 | a | 0.18 |
3 | 30≤x<40 | 20 | b |
4 | 40≤x<50 | 16 | 0.32 |
合计 | 1 |
(1)表中a= , b=;
(2)这个样本数据的中位数在第组;
(3)下表为≤体育与健康≥中考察“排球30秒对墙垫球”的中考评分标准,若该校九年级有500名学生,请你估计该校九年级学生在这一项目中得分在7分以上(包括7分)学生约有多少人? 排球30秒对墙垫球的中考评分标准
分值 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
排球(个) | 40 | 36 | 33 | 30 | 27 | 23 | 19 | 15 | 11 | 7 |




