题目内容
【题目】已知二次函数y=x2+2x﹣3.

(1)将二次函数y=x2+2x﹣3化成顶点式.
(2)求图象与x轴,y轴的交点坐标.
(3)在坐标系中利用描点法画出此抛物线.
(4)当x取何值时,y随x的增大而减小?
【答案】(1)y=(x+1)2﹣4;(2)该抛物线与x轴的交点坐标是(﹣3,0)(1,0);(3)见解析;(4)当x<﹣1时,y随x的增大而减小.
【解析】
(1)把解析式配方后即可得答案;(2)令x=0,可得图象与y轴的交点,把二次函数解析式化成两点式,即可得图象与x轴的交点;(3)分别代入x=-3、-2、-1、0、1,求出y值,在坐标系中描点,用平滑曲线连接即可;(4)根据顶点式可知对称轴为x=-1,根据图象开口方向即可得答案.
(1)y=x2+2x﹣3=x2+2x+1﹣3﹣1=(x+1)2﹣4,即y=(x+1)2﹣4.
(2)令x=0,则y=﹣3,即该抛物线与y轴的交点坐标是 (0,﹣3),
∵y= x2+2x﹣3=(x+3)(x﹣1),
∴该抛物线与x轴的交点坐标是(﹣3,0)(1,0).
(3)列表:
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | … |
y | … | 0 | ﹣3 | ﹣4 | ﹣3 | 0 | … |
图象如图所示:
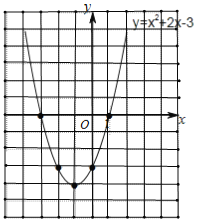
(4)∵二次函数解析式为y=(x+1)2﹣4,
∴对称轴为直线x=﹣1,
∵抛物线开口向上,
∴当x<﹣1时,y随x的增大而减小.

练习册系列答案
相关题目