题目内容
【题目】小明身高为1.6米,通过地面上的一块平面镜C,刚好能看到前方大树的树梢E,此时他测得俯角为45度,然后他直接抬头观察树梢E,测得仰角为30度.求树的高度.(结果保留根号) 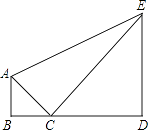
【答案】解:设树的高度为x米,过点A作DE的垂线,垂足为F,
∵由题意得△ABC与△CDE都是直角三角形,
∴AB=BC=1.6米,CD=DE=x.
∵∠B=∠D=∠AFD=90°,
∴四边形ABDF是矩形,
∴AF=BD=x+1.6,DE=AB=1.6,EF=x﹣1.6.
∵∠EAF=30°,
∴tan∠EAF= ![]() =
= ![]() =
= ![]() ,解得x=
,解得x= ![]() .
.
答:树的高度为 ![]() 米.
米.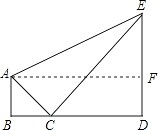
【解析】设树的高度为x米,过点A作DE的垂线,垂足为F,再根据∠B=∠D=∠AFD=90°得出四边形ABDF是矩形,由锐角三角函数的定义即可得出结论.
【考点精析】解答此题的关键在于理解关于仰角俯角问题的相关知识,掌握仰角:视线在水平线上方的角;俯角:视线在水平线下方的角.

练习册系列答案
相关题目