题目内容
【题目】观察图,解答下列问题.
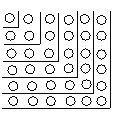
(1)图中的小圆圈被折线隔开分成六层,第一层有1个小圆圈,第二层有3个圆圈,第三层有5个圆圈,……,第六层有11个圆圈.如果要你继续
下去,那么第七层有几个小圆圈?第n层呢?
(2)某一层上有77个圆圈,这是第几层?
(3)数图中的圆圈个数可以有多种不同的方法.
比如:前两层的圆圈个数和为(1+3)或22,
由此得,1 + 3 = 22.
同样,
由前三层的圆圈个数和得:1 + 3 + 5 = 32.
由前四层的圆圈个数和得:1 + 3 + 5 + 7 = 42.
由前五层的圆圈个数和得:1 + 3 + 5 + 7 + 9 = 52.
……
根据上述请你猜测,从1开始的n个连续奇数之和是多少?用公式把它表示出来.
(4)计算:1 + 3 + 5 + … + 19的和;
(5)计算:11 + 13 + 15 + … + 99的和.
【答案】(1)13个;(2n-1)个;(2)39层;(3)n2;(4)100;(5)2475.
【解析】
(1)根据已知数据即可得出每一层小圆圈个数是连续的奇数,进而得出答案;
(2)利用(1)中发现的规律得出答案即可;
(3)利用已知数据得出答案即可;
(4)利用(3)中发现的规律得出答案即可;
(5)利用(3)中发现的规律得出答案即可.
(1)第七层有13个小圆圈,第n层有(2n-1)个小圆圈,
(2)令2n-1 = 77,得,n = 39,
所以,这是第39层;
(3)1 + 3 + 5 + … +(2n-1)= n2
(4)1 + 3 + 5 + … + 19 = 102 = 100;
(5)11 + 13 + 15 + … + 99 = (1 + 3 + 5 + …… + 99)-(1 + 3 + 5 + …… + 9)= 502 -52 = 2475