题目内容
【题目】如图,在![]() 中,
中,![]() 是直径,
是直径,![]() 是切线,点
是切线,点![]() 为切点.
为切点.
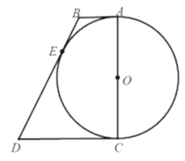
(1)求证:![]() ;
;
(2)如图,连接![]() 交于点
交于点![]() ,连接
,连接![]() 并延长,交
并延长,交![]() 于点
于点![]() ,求证:
,求证:![]() ;
;

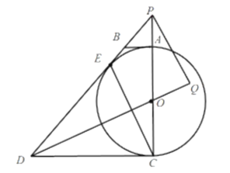
(3)如图,延长![]() 交于点
交于点![]() 连接
连接![]() 过点
过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() .若
.若![]()
![]() 求
求![]() 的长.
的长.
【答案】(1)见解析;(2)见解析;(3)![]()
【解析】
(1)利用全等的性质证得∠BOD=90![]() ,再证得Rt△BOE
,再证得Rt△BOE![]() Rt△ODE,再利用等量代换即可证明结论;
Rt△ODE,再利用等量代换即可证明结论;
(2)证得![]() ,利用平行线分线段成比例定理结合等量代换即可证明结论;
,利用平行线分线段成比例定理结合等量代换即可证明结论;
(3)在![]() 中,利用勾股定理求得PC的长,求得
中,利用勾股定理求得PC的长,求得![]() ,推出
,推出![]() 和
和![]() ,求得
,求得![]() ,再推出
,再推出![]() ,在
,在![]() 和
和![]() 中,利用余弦函数即可求解.
中,利用余弦函数即可求解.
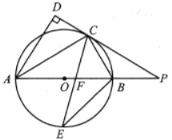
(1)证明:如图,连接OB、OE、OD.
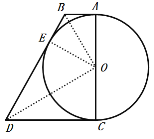
∵AB、BD、CD是![]() 的切线,
的切线,
∴BA=BE,∠BEO=∠BAO=90![]() ,DC=DE,
,DC=DE,
在Rt△BEO和Rt△BAO中,
![]() ,
,
∴![]() ,
,
∴![]() ,
,
同理可得![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴Rt△BOE![]() Rt△ODE,
Rt△ODE,
∴![]() ,
,
∴![]() ,
,
∵![]()
∴![]() ;
;
(2)证明:∵AB、CD是![]() 的切线,
的切线,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ;
;
(3)解:∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() ①,
①,
∵![]() ,
,
∴![]() ②,
②,
联立①②并解得:
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() .
.

练习册系列答案
相关题目