题目内容
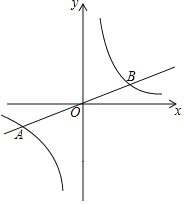
【题目】如图,点A(-3,0)、点B(0,![]() ),直线
),直线![]() 与x轴、y轴分别交于点D、C,M是平面内一动点,且∠AMB=60°,则MCD面积的最小值是 ________.
与x轴、y轴分别交于点D、C,M是平面内一动点,且∠AMB=60°,则MCD面积的最小值是 ________.

【答案】![]()
【解析】
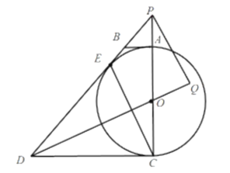
由直线方程求出点D、C的坐标,由已知M是平面内一动点,且∠AMB=60知点M在ΔABM的外接圆上,由已知推导出AB∥CD,则可知要使ΔMCD面积最小,只需点M在AB的垂直平分线上,进而证得ΔABM是等边三角形,通过推理求出点M坐标,即可求得面积最小值.
∵M是平面内一动点,且∠AMB=60,
∴点M在ΔABM的外接圆上,
∵直线![]() 与x轴、y轴分别交于点D、C,
与x轴、y轴分别交于点D、C,
∴C(0,![]() ),D(4,0),
),D(4,0),
∴OC=![]() ,OD=4,
,OD=4,
∴tan∠ODC=![]() ,
,
∴∠ODC=60,
∵点A(-3,0)、点B(0,![]() ),
),
∴OA=3,OB=![]() ,
,
∴tan∠OAB=![]() ,且AB=
,且AB=![]() ,
,
∴∠OAB=60,
∴AB∥CD ,
∴当M在AB的垂直平分线上时,ΔMCD的面积最小,此时AM=BM,
∵∠AMB=60,
∴ΔAMB是等边三角形,
∴∠BAM=60,
∴点M在x轴上,且AM=AB=6,
∴点M(3,0)
∴MD=1,
∴ΔMCD的面积最小值为![]() ,
,
故答案为:![]() .
.

练习册系列答案
相关题目
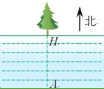
【题目】小明投资销售一种进价为每件20元的护眼台灯.经过市场调研发现,每月销售的数量y(件)是售价x(元/件)的一次函数,其对应关系如表:
x/(元/件) | 22 | 25 | 30 | 35 | … |
y/件 | 280 | 250 | 200 | 150 | … |
在销售过程中销售单价不低于成本价,物价局规定每件商品的利润不得高于成本价的60%,
(1)请求出y关于x的函数关系式.
(2)设小明每月获得利润为w(元),求每月获得利润w(元)与售价x(元/件)之间的函数关系式,并确定自变量x的取值范围.
(3)当售价定为多少元/件时,每月可获得最大利润,最大利润是多少?