Question

【题目】如图，在等腰 Rt△ABC 中，∠ACB=90°，P 是射线CB上一点(在B点右侧)，连接AP，延长PC至点Q，使得 CQ=CP，过点Q作QH⊥AP交PA延长线于点H，交BA延长线于点M，用等式表示线段MB与PQ之间的数量关系，并证明.

Answer 1

【答案】，证明见解析.

【解析】

过M作MD⊥PQ，连接AQ，由垂直平分线的性质可得AQ=AP，设∠PAB==∠MAH，利用角度关系可推出∠QAM==∠AMQ，进而得到AQ=QM，再证明△QMD≌△APC得到MD= PC=PQ，最后根据△MDB为等腰直角三角形可得出MB与PQ之间的关系.

解：，证明如下：

如图所示，过M作MD⊥PQ，连接AQ，

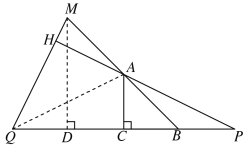
∵∠ACB=90°，CQ=CP

∴AC垂直平分PQ，

∴AQ=AP，

∴∠QAC=∠PAC，

设∠PAB==∠MAH，∵△ABC为等腰直角三角形

∴∠QAC=∠PAC=45°+，

∴∠QAH=180°-∠QAC-∠PAC=

∴∠QAM=∠QAH+∠MAH=

∵PH⊥QM，

∴∠MHA=90°，

∴∠AMQ=

∴∠QAM=∠AMQ

∴AQ=QM

又∵AQ=AP

∴QM=AP

∵∠P+∠MQD=90°，∠QMD+∠MQD=90°，

∴∠QMD=∠P

在△QMD和△APC中，

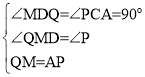
∴△QMD≌△APC（AAS）

∴MD=PC=PQ

∵∠MDB=90°，∠MBD=45°，

∴△MDB为等腰直角三角形

∴MB=MD=PQ

即PQ=MB.