题目内容
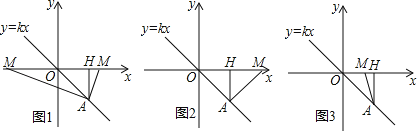
【题目】已知正比例函数y=kx经过点A,点A在第四象限,过点A作AH⊥x轴,垂足为点H,点A的横坐标为3,且△AOH的面积为3.

(1)求正比例函数的表达式;
(2)在x轴上能否找到一点M,使△AOM是等腰三角形?若存在,求点M的坐标;若不存在,请说明理由.
【答案】(1)y=﹣![]() x;(2)当点M的坐标为(﹣
x;(2)当点M的坐标为(﹣![]() ,0)、(
,0)、(![]() ,0)、(6,0)或(
,0)、(6,0)或(![]() ,0)时,△AOM是等腰三角形.
,0)时,△AOM是等腰三角形.
【解析】
(1)根据点A的横坐标、△AOH的面积结合点A所在的象限,即可得出点A的坐标,再利用待定系数法即可求出正比例函数的表达式;
(2)分OM=OA、AO=AM、OM=MA三种情况考虑,①当OM=OA时,根据点A的坐标可求出OA的长度,进而可得出点M的坐标;②当AO=AM时,由点H的坐标可求出点M的坐标;③当OM=MA时,设OM=x,则MH=3﹣x,利用勾股定理可求出x值,进而可得出点M的坐标.综上即可得出结论.
解:(1)∵点A的横坐标为3,△AOH的面积为3,点A在第四象限,
∴点A的坐标为(3,﹣2).
将A(3,﹣2)代入y=kx,
﹣2=3k,解得:k=﹣![]() ,
,
∴正比例函数的表达式为y=﹣![]() x.
x.
(2)①当OM=OA时,如图1所示,
∵点A的坐标为(3,﹣2),
∴OH=3,AH=2,OA=![]() =
=![]() ,
,
∴点M的坐标为(﹣![]() ,0)或(
,0)或(![]() ,0);
,0);
②当AO=AM时,如图2所示,
∵点H的坐标为(3,0),
∴点M的坐标为(6,0);
③当OM=MA时,设OM=x,则MH=3﹣x,
∵OM=MA,
∴x=![]() ,
,
解得:x=![]() ,
,
∴点M的坐标为(![]() ,0).
,0).
综上所述:当点M的坐标为(﹣![]() ,0)、(
,0)、(![]() ,0)、(6,0)或(
,0)、(6,0)或(![]() ,0)时,△AOM是等腰三角形.
,0)时,△AOM是等腰三角形.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目