题目内容
【题目】平行四边形 ABCD 中,两条邻边长分别为3和5,∠BAD与∠ABC的平分线交于点E,点F 是CD的中点,连接EF,则EF=________.
【答案】3.5或0.5
【解析】
分两种情况讨论:①当AB=3,BC=5时,延长AE交BC于M,由平行线的性质和角平分线的定义可推出∠BAM=∠AMB,得到AB=BM=3,求出CM=2,再证明∠AEB=90°,根据等腰三角形三线合一得到E为AM的中点,所以EF为梯形ADCM的中位线,根据中位线的性质可求EF;②当AB=5,BC=3时,延长AE交BC的延长线于M,连接DM,延长EF与DM交于G,同理可证AE=EM,CM=2,再利用三角形中位线的性质可求出EF.
分两种情况:
①如图1,当AB=3,BC=5时,延长AE交BC于M,
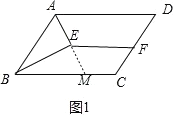
∵AD∥BC,
∴∠DAM=∠AMB
∵AM平分∠BAD,
∴∠DAM=∠BAM
∴∠BAM=∠AMB
∴AB=BM=3
∴CM=BC-BM=5-3=2
∵AD∥BC
∴∠DAB+∠ABC=180°
又∵AE平分∠BAD,BE平分∠ABC,
∴∠EAB+∠EBA=![]() ∠DAB+
∠DAB+![]() ∠ABC=90°,
∠ABC=90°,
∴∠AEB=90°
∴BE⊥AM,
∵BA=BM
∴AE=EM
∵DF=CF
∴EF为梯形ADCM的中位线
∴EF=![]()
②如图,当AB=5,BC=3时,
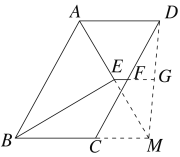
延长AE交BC的延长线于M,连接DM,延长EF与DM交于G,
同①可证:AE=EM,CM=BM-BC=AB-BC=2,
EG为△ADM的中位线,FG为△CDM的中位线,
∴EG=![]() AD=1.5,FG=
AD=1.5,FG=![]() CM=1,
CM=1,
∴EF=EG-FG=0.5
综上所述,EF的长为3.5或0.5
故答案为:3.5或0.5

练习册系列答案
相关题目