��Ŀ����
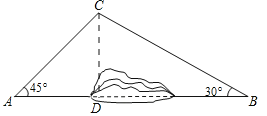
����Ŀ��Ϊ�ӿ����Խӣ�����������壬ij������A��B���ؼ�Ĺ�·���иĽ�����ͼ��A��B����֮����һ��ɽ������ԭ����A�ص�B����;��C��������ACB��ʻ���ֿ�ͨ������������ֱ����ֱ��AB��ʻ����֪BC��80ǧ�ף���A��45�㣬��B��30�㣮
(1)��ͨ����ǰ��������A�ص�B��Ҫ�߶���ǧ�ף�
(2)��ͨ������������A�ص�B�ؿ������߶���ǧ�ף�(�����������)

���𰸡�(1)��ͨ����ǰ��������A�ص�B��Ҫ��(80+40![]() )ǧ�ף�(2)������A�ص�B�ر�ԭ�����ߵ�·��Ϊ[40+40(
)ǧ�ף�(2)������A�ص�B�ر�ԭ�����ߵ�·��Ϊ[40+40(![]() ��
��![]() )]ǧ�ף�
)]ǧ�ף�
��������
��1������C��AB�Ĵ���CD������ΪD����ֱ����ACD�У���ֱ�����������CD��������ɣ�
��2����ֱ����CBD�У���ֱ�����������BD�������AD���������������A�ص�B�ر�ԭ�����߶���·�̣�
(1)����C��AB�Ĵ���CD������ΪD��
��AB��CD��sin30����![]() ��BC��80ǧ�ף�
��BC��80ǧ�ף�
��CD��BCsin30����80��![]() ��40(ǧ��)��
��40(ǧ��)��
AC��![]() (ǧ��)��
(ǧ��)��
AC+BC��80+![]() (ǧ��)��
(ǧ��)��
�𣺿�ͨ����ǰ��������A�ص�B��Ҫ��(80+![]() )ǧ�ף�
)ǧ�ף�
(2)��cos30����![]() ��BC��80(ǧ��)��
��BC��80(ǧ��)��
��BD��BCcos30����80��![]() (ǧ��)��
(ǧ��)��
��tan45����![]() ��CD��40(ǧ��)��
��CD��40(ǧ��)��
��AD��![]() (ǧ��)��
(ǧ��)��
��AB��AD+BD��40+![]() (ǧ��)��
(ǧ��)��
��������A�ص�B�ر�ԭ�����߶���·��Ϊ��AC+BC��AB��80+![]() ��40��
��40��![]() ��40+40
��40+40![]() (ǧ��)��
(ǧ��)��
��������A�ص�B�ر�ԭ�����ߵ�·��Ϊ [40+40![]() ]ǧ�ף�
]ǧ�ף�

 ������ҵ����ν�����������ϵ�д�
������ҵ����ν�����������ϵ�д�