题目内容
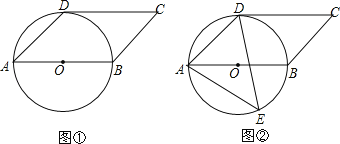
【题目】已知四边形ABCD是平行四边形,以AB为直径的⊙O经过点D,∠DAB=45°.
(1)如图①,判断CD与⊙O的位置关系,并说明理由;
(2)如图②,E是⊙O上一点,且点E在AB的下方,若⊙O的半径为3cm,AE=5cm,求点E到AB的距离.
【答案】(1)CD与圆O相切,证明见解析;(2)EF=![]() .
.
【解析】
(1)连接OD,由题意可得∠AOD=90°,由平行线的性质可得OD⊥CD,则可得结论;
(2)作EF⊥AB于F,连接BE,由圆周角定理可得∠AEB=90°,由勾股定理可求BE的长,由三角函数可求EF的长.
解:
(1)CD与圆O相切
证明:如图①,连接OD,
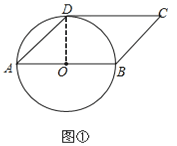
∵OA=OD
∴∠DAB=∠ADO=45°
∴∠AOD=90°,
∵四边形ABCD是平行四边形,
∴AB∥DC.
∴∠CDO=∠AOD=90°.
∴OD⊥CD
∴CD与圆O相切
(2)如图②,作EF⊥AB于F,连接BE,
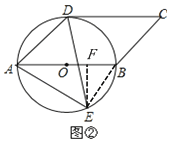
∵AB是圆O的直径,
∴∠AEB=90°,AB=2×3=6
∵AE=5
∴BE=![]()
∵sin∠BAE=![]()
∴![]()
∴EF=![]()

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
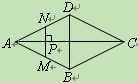
期末集结号系列答案【题目】如图,点P是菱形ABCD的对角线AC上的一个动点,过点P垂直于AC的直
线交菱形ABCD的边于M、N两点.设AC=2,BD=1,AP=x,△AMN的面积为y,则
y关于x的函数图象大致形状是【 】

【题目】某校的一个社会实践小组对本校学生中开展主题为“垃圾分类知多少”的专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为“非常了解”、“比较了解”、“基本了解”、“不太了解”四个等级,划分等级后的数据整理如下表:
等级 | 非常了解 | 比较了解 | 基本了解 | 不太了解 |
频数 | 20 | 35 | 41 | 4 |
(1)请根据调查结果,若该校有学生![]() 人,请估计这些学生中“比较了解”垃圾分类知识的人数.
人,请估计这些学生中“比较了解”垃圾分类知识的人数.
(2)在“比较了解”的调查结果里,其中九(1)班学生共有![]() 人,其中
人,其中![]() 名男生和
名男生和![]() 名女生,在这
名女生,在这![]() 人中,打算随机选出
人中,打算随机选出![]() 位进行采访,求出所选两位同学恰好是1名男生和1名女生的概率.(要求列表或画树状图)
位进行采访,求出所选两位同学恰好是1名男生和1名女生的概率.(要求列表或画树状图)