题目内容
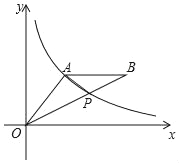
【题目】如图,A(3,m)是反比例函数y=![]() 在第一象限图象上一点,连接OA,过A作AB∥x轴,连接OB,交反比例函数y=
在第一象限图象上一点,连接OA,过A作AB∥x轴,连接OB,交反比例函数y=![]() 的图象于点P(2
的图象于点P(2![]() ,
,![]() ).
).
(1)求m的值和点B的坐标;
(2)连接AP,求△OAP的面积.
【答案】(1)m=4,点B的坐标为(8,4);(2)5![]() .
.
【解析】
(1)将点P的坐标代入解析式求解可得解析式,再把A点的坐标代入得到m的值,利用勾股定理求得AB=OA=5,由AB∥x轴即可得点B的坐标;
(2)根据点B坐标和点P的坐标,得到AE=1、PE=3![]() 、PD=
、PD=![]() ,再利用割补法求解可得.
,再利用割补法求解可得.
(1)将P(2![]() ,
,![]() )代入y═
)代入y═![]() ,得:k=12,
,得:k=12,
则反比例函数解析式为y=![]() ,
,
把A(3,m)代入y=![]() 得m=4,
得m=4,
如图,过点A作AC⊥x轴于点C,
则OC=3、AC=4,
∴OA=![]() =5,
=5,
∵AB∥x轴,且AB=OA=5,
∴点B的坐标为(8,4);
(3)∵点B坐标为(8,4),
点P坐标为(2![]() ,
,![]() ),
),
过点P作PD⊥x轴,延长DP交AB于点E,
则点E坐标为(2![]() ,4),
,4),
∴AE=2![]() ﹣3、PE=4﹣
﹣3、PE=4﹣![]() 、PD=
、PD=![]() ,
,
则△OAP的面积=![]() ×(4+
×(4+![]() )×(2
)×(2![]() ﹣3)=5
﹣3)=5![]() .
.

练习册系列答案
相关题目