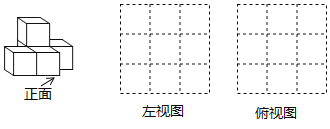
题目内容
【题目】点D是等边三角形ABC外一点,且DB=DC,∠BDC=120°,将一个三角尺60°角的顶点放在点D上,三角尺的两边DP,DQ分别与射线AB,CA相交于E,F两点.
(1)当EF∥BC时,如图①所示,求证:EF=BE+CF.
(2)当三角尺绕点D旋转到如图②所示的位置时,线段EF,BE,CF之间的上述数量关系是否成立?如果成立,请说明理由;如果不成立,写出EF,BE,CF之间的数量关系,并说明理由.
(3)当三角尺绕点D继续旋转到如图③所示的位置时,(1)中的结论是否发生变化?如果不变化,直接写出结论;如果变化,请直接写出EF,BE,CF之间的数量关系.
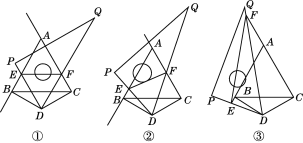
【答案】(1)见解析;(2)结论仍然成立.理由见解析;(3)结论发生变化.EF=CF-BE.
【解析】
(1)根据△ABC是等边三角形知道AB=AC,∠ABC=∠ACB=60°,而DB=DC,∠BDC=120°,这样可以得到△DCF和△BED是直角三角形,由于EF∥BC,可以证明△AEF是等边三角形,也可以证明△BDE≌△CDF,可以得到DE=DF,由此进一步得到
DE=DF∠BDE=∠CDF=30°,这样可以得到BE=![]() DE=
DE=![]() DF=CF,而△DEF是等边三角形,所以题目的结论就可以证明出来了;(2)结论仍然成立.如图,在AB的延长线上取点F’,使BF’=CF,连接DF’,根据(1)的结论可以证明△DCF≌△DBF’,根据全等三角形的性质可以得到DF=DF’,∠BDF’=∠CDF,又∠BDC=120°,∠EDF=60°,可以得到:∠EDF’=∠CDF=60°,由此可以证明△EDF’≌△EDF,从而证明题目的结论;(3)结论发生变化. EF=BE-CF.如图,在射线AB上取点F′,使BF′=CF,连接DF′.由(1)得△DCF≌△DBF′(SAS).根据全等三角形的性质可以得到DF=DF′,∠BDF′=∠CDF.又因为∠BDC=120°,∠EDF=60°,可以得到∠FDB+∠CDF=60°,∠FDB+∠BDF′=∠FDF′=120°,所以∠EDF′=∠EDF=60°,由此可得△EDF′≌△EDF(SAS),从而证明题目的结论EF=EF′=BF′- BE=CF- BE。
DF=CF,而△DEF是等边三角形,所以题目的结论就可以证明出来了;(2)结论仍然成立.如图,在AB的延长线上取点F’,使BF’=CF,连接DF’,根据(1)的结论可以证明△DCF≌△DBF’,根据全等三角形的性质可以得到DF=DF’,∠BDF’=∠CDF,又∠BDC=120°,∠EDF=60°,可以得到:∠EDF’=∠CDF=60°,由此可以证明△EDF’≌△EDF,从而证明题目的结论;(3)结论发生变化. EF=BE-CF.如图,在射线AB上取点F′,使BF′=CF,连接DF′.由(1)得△DCF≌△DBF′(SAS).根据全等三角形的性质可以得到DF=DF′,∠BDF′=∠CDF.又因为∠BDC=120°,∠EDF=60°,可以得到∠FDB+∠CDF=60°,∠FDB+∠BDF′=∠FDF′=120°,所以∠EDF′=∠EDF=60°,由此可得△EDF′≌△EDF(SAS),从而证明题目的结论EF=EF′=BF′- BE=CF- BE。
(1)证明:∵△ABC是等边三角形,
∴AB=AC,∠ABC=∠ACB=60°.
∵DB=DC,∠BDC=120°,
∴∠DBC=∠DCB=30°.
∴∠DBE=∠DBC+∠ABC=90°,
∠DCF=∠DCB+∠ACB=90°.
∵EF∥BC,∴∠AEF=∠ABC=60°,
∠AFE=∠ACB=60°.∴AE=AF.
∴BE=AB-AE=AC-AF=CF.
又∵DB=DC,∠DBE=∠DCF=90°,
∴△BDE≌△CDF.
∴DE=DF,∠BDE=∠CDF=![]() (120°-60°)=30°.
(120°-60°)=30°.
∴BE=![]() DE=
DE=![]() DF=CF.
DF=CF.
∵∠EDF=60°,∴△DEF是等边三角形,
即DE=DF=EF.
∴BE+CF=![]() DE+
DE+![]() DF=EF,
DF=EF,
即EF=BE+CF.
(2)解:结论仍然成立.
理由如下:如图,在射线AB上取点F′,
使BF′=CF,连接DF′.
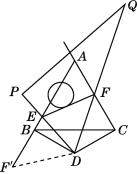
由(1)得∠DBE=∠DCF=90°,
则∠DBF′=∠DCF=90°.
又∵BD=CD,
∴△DCF≌△DBF′(SAS).
∴DF=DF′,∠BDF′=∠CDF.
又∵∠BDC=120°,∠EDF=60°,
∴∠EDB+∠CDF=60°.
∴∠EDB+∠BDF′=∠EDF′=60°.
∴∠EDF′=∠EDF.
又∵DE=DE,
∴△EDF′≌△EDF(SAS).
∴EF=EF′=BE+BF′=BE+CF.
(3)解:结论发生变化.EF=CF-BE.
理由:在射线AB上取点F′,
使BF′=CF,连接DF′.
由(1)得∠DBA=∠DCF=90°,
则∠DBF′=∠DCF=90°.
又∵BD=CD,
∴△DCF≌△DBF′(SAS).
∴DF=DF′,∠BDF′=∠CDF.
又∵∠BDC=120°,∠EDF=60°,
∴∠FDB+∠CDF=60°.
∴∠FDB+∠BDF′=∠FDF′=120°.
∴∠EDF′=∠EDF=60°.
又∵DE=DE,DF=DF′,
∴△EDF′≌△EDF(SAS).
∴EF=EF′=BF′- BE=CF- BE。


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案【题目】如图,用正方形是墩垒石梯,下图分别表示垒到一、二阶梯时的情况,那么照这样垒下去
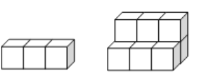
一级 二级
①填出下表中未填的两空,观察规律。
阶梯级数 | 一级 | 二级 | 三级 | 四级 |
石墩块数 | 3 | 9 |
②到第n级阶梯时,共用正方体石墩_______________块(用n的代数式表示)