题目内容
【题目】已知:二次函数y=ax2+2ax﹣4(a≠0)的图象与x轴交于点A,B(A点在B点的左侧),与y轴交于点C,△ABC的面积为12.
(1)求二次函数图象的对称轴与它的解析式;
(2)点D在y轴上,当以A、O、D为顶点的三角形与△BOC相似时,求点D的坐标;
(3)点D的坐标为(﹣2,1),点P在二次函数图象上,∠ADP为锐角,且tan∠ADP=2,求点P的横坐标.

【答案】(1)y=![]() x2+x﹣4;(2)点D的坐标为(0,2)或(0,﹣2)或(0,8)或(0,﹣8);(3)P点的横坐标为﹣2或
x2+x﹣4;(2)点D的坐标为(0,2)或(0,﹣2)或(0,8)或(0,﹣8);(3)P点的横坐标为﹣2或![]() .
.
【解析】分析:![]() 根据对称轴坐标公式可求二次函数图象的对称轴;当x=0时,y=4,可求点C的坐标为(0,4),,根据三角形面积公式可求
根据对称轴坐标公式可求二次函数图象的对称轴;当x=0时,y=4,可求点C的坐标为(0,4),,根据三角形面积公式可求![]() 进一步得到A点和B点的坐标分别为(4,0),(2,0).待定系数法可求二次函数的解析式.
进一步得到A点和B点的坐标分别为(4,0),(2,0).待定系数法可求二次函数的解析式.
![]()
![]() 则分
则分![]() 和
和![]() 两种情况讨论即可.
两种情况讨论即可.
![]() 过D作
过D作![]() 轴于F,分两种情况:①当点P在直线AD的下方时,②当点P在直线AD的上方时.分别求解.
轴于F,分两种情况:①当点P在直线AD的下方时,②当点P在直线AD的上方时.分别求解.
详解:(1)该二次函数的对称轴是:直线![]()
当x=0时,y=4,
∴点C的坐标为(0,4),
∴![]()
连接![]()
∵![]()
![]()
又∵点A,B关于直线x=1对称,
∴A点和B点的坐标分别为(4,0),(2,0).
∴4a+4a4=0,解得![]()
∴所求二次函数的解析式为![]()
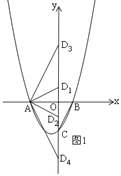
(2)如图1,∵![]()
且![]()
![]()
分两种情况:
①当![]() 时,
时,![]()
∴![]()
即![]() 或
或![]()
②当![]() 时,
时,![]()
∴![]()
即![]() 或
或![]()
综上所述,点D的坐标为![]() 或
或![]() 或
或![]() 或
或![]() ;
;
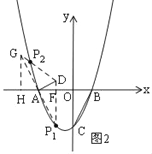
(3)如图2,过D作![]() 轴于F,分两种情况:
轴于F,分两种情况:
①当点P在直线AD的下方时,如图所示:
由(1)得点A(4,0),点D(2,1),
∴DF=1,AF=2.
在Rt△ADF中,![]() 得
得![]()
延长DF与抛物线交于点![]() ,则
,则![]() 点为所求,
点为所求,
∴点![]() 的坐标为(2,4).
的坐标为(2,4).
②当点P在直线AD的上方时,延长P1A至点G使得AG=AP1,连接DG,作GH⊥x轴于点H,如图所示.
可证△GHA≌△P1FA.
∴HA=AF,GH=P1F,GA=P1A.
又∵A(4,0),P1(2,4),
∴点G的坐标是(6,4).
易得DG的解析式为:![]()
在![]() 中,
中,![]()
∴![]()
∴![]()
∴![]()
∴![]()
∴![]()
∴![]()
设DG与抛物线的交点为P2,则P2点为所求,设![]()
代入DG的解析式中,![]()
解得![]()
∵P2 点在第二象限,
∴P2点的横坐标为![]() (舍正)
(舍正)
综上,P点的横坐标为![]() 或
或![]() .
.

 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案【题目】如图,用正方形是墩垒石梯,下图分别表示垒到一、二阶梯时的情况,那么照这样垒下去
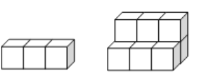
一级 二级
①填出下表中未填的两空,观察规律。
阶梯级数 | 一级 | 二级 | 三级 | 四级 |
石墩块数 | 3 | 9 |
②到第n级阶梯时,共用正方体石墩_______________块(用n的代数式表示)
【题目】为了了解某校学生的课外阅读情况,随机抽查了![]() 名学生周阅读用时数,结果如下表:
名学生周阅读用时数,结果如下表:
周阅读用时数(小时) | 4 | 5 | 8 | 12 |
学生人数(人) | 3 | 4 | 2 | 1 |
则关于这![]() 名学生周阅读所用时间,下列说法正确的是( )
名学生周阅读所用时间,下列说法正确的是( )
A. 中位数是![]() B. 众数是
B. 众数是![]() C. 平均数是
C. 平均数是![]() D. 方差是
D. 方差是![]()