题目内容
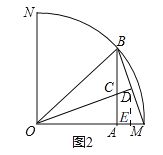
【题目】如图1,已知扇形MON的半径为![]() ,∠MON=90°,点B在弧MN上移动,联结BM,作OD⊥BM,垂足为点D,C为线段OD上一点,且OC=BM,联结BC并延长交半径OM于点A,设OA=x,∠COM的正切值为y.
,∠MON=90°,点B在弧MN上移动,联结BM,作OD⊥BM,垂足为点D,C为线段OD上一点,且OC=BM,联结BC并延长交半径OM于点A,设OA=x,∠COM的正切值为y.
(1)如图2,当AB⊥OM时,求证:AM=AC;
(2)求y关于x的函数关系式,并写出定义域;
(3)当△OAC为等腰三角形时,求x的值.

【答案】 (1)证明见解析;(2) ![]() .(
.(![]() );(3)
);(3) ![]() .
.
【解析】分析:(1)先判断出∠ABM=∠DOM,进而判断出△OAC≌△BAM,即可得出结论;
(2)先判断出BD=DM,进而得出![]() ,进而得出AE=
,进而得出AE=![]() ,再判断出
,再判断出![]() ,即可得出结论;
,即可得出结论;
(3)分三种情况利用勾股定理或判断出不存在,即可得出结论.
详解:(1)∵OD⊥BM,AB⊥OM,∴∠ODM=∠BAM=90°.
∵∠ABM+∠M=∠DOM+∠M,∴∠ABM=∠DOM.
∵∠OAC=∠BAM,OC=BM,∴△OAC≌△BAM,
∴AC=AM.
(2)如图2,过点D作DE∥AB,交OM于点E.
∵OB=OM,OD⊥BM,∴BD=DM.
∵DE∥AB,∴![]() ,∴AE=EM.∵OM=
,∴AE=EM.∵OM=![]() ,∴AE=
,∴AE=![]() .
.
∵DE∥AB,∴![]() ,
,
∴![]() .(
.(![]() )
)
(3)(i) 当OA=OC时.∵![]() .在Rt△ODM中,
.在Rt△ODM中,![]() .
.
∵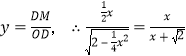 .解得
.解得![]() ,或
,或![]() (舍).
(舍).
(ii)当AO=AC时,则∠AOC=∠ACO.∵∠ACO>∠COB,∠COB=∠AOC,∴∠ACO>∠AOC,∴此种情况不存在.
(ⅲ)当CO=CA时,则∠COA=∠CAO=α.∵∠CAO>∠M,∠M=90°﹣α,∴α>90°﹣α,∴α>45°,∴∠BOA=2α>90°.∵∠BOA≤90°,∴此种情况不存在.
即:当△OAC为等腰三角形时,x的值为![]() .
.

 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案【题目】为了了解某校学生的课外阅读情况,随机抽查了![]() 名学生周阅读用时数,结果如下表:
名学生周阅读用时数,结果如下表:
周阅读用时数(小时) | 4 | 5 | 8 | 12 |
学生人数(人) | 3 | 4 | 2 | 1 |
则关于这![]() 名学生周阅读所用时间,下列说法正确的是( )
名学生周阅读所用时间,下列说法正确的是( )
A. 中位数是![]() B. 众数是
B. 众数是![]() C. 平均数是
C. 平均数是![]() D. 方差是
D. 方差是![]()