题目内容
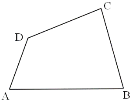
【题目】定义:有三个内角相等的四边形叫三等角四边形.
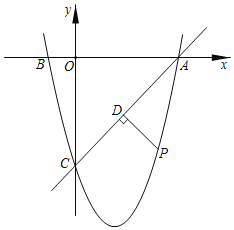
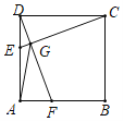
(1)如图,折叠平行四边形纸片![]() ,使顶点
,使顶点![]() ,
,![]() 别落在边
别落在边![]() ,
,![]() 的点
的点![]() ,
,![]() 处,折痕分别为
处,折痕分别为![]() ,
,![]() .求证:四边形
.求证:四边形![]() 是三等角四边形;
是三等角四边形;
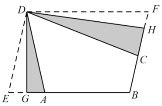
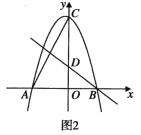
(2)当![]() 时,如图所示,在三等角四边形
时,如图所示,在三等角四边形![]() 中,
中,![]() ,若
,若![]() ,设
,设![]() ,
,![]() ,求y与x的函数关系式,并求出
,求y与x的函数关系式,并求出![]() 的最大值是多少?
的最大值是多少?
【答案】(1)证明见解析;(2)![]() ,AB最大值是
,AB最大值是![]() .
.
【解析】
(1)由四边形 ![]() 是平行四边形,得到
是平行四边形,得到![]() ,且
,且![]() ,再根据等角的补角相等,判断出
,再根据等角的补角相等,判断出![]() 即可;
即可;
(2)计算出AB的长,从而得到当AD=2时,AB最长,最后计算出对角线AC的长.
(1)![]() 四边形
四边形 ![]() 是平行四边形,
是平行四边形,
![]() ,
,![]() ,
,
有折叠,得 ![]() ,
,![]() .
.
![]() .
.
![]() .
.
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() 四边形
四边形 ![]() 是三等角四边形.
是三等角四边形.
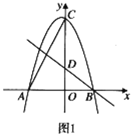
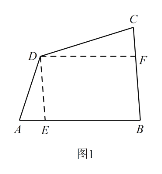
(2)当 ![]() 时,如图 1 所示,过点
时,如图 1 所示,过点 ![]() 作
作 ![]() 交
交 ![]() 于点
于点 ![]() ,作
,作 ![]() 交
交 ![]() 于点
于点 ![]() .
.
![]() 四边形
四边形 ![]() 是平行四边形,
是平行四边形,![]() ,
,
![]() ,
,![]() .
.
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
设 ![]() ,
,![]() ,则
,则 ![]() ,
,![]() ,
,
由 ![]() ,得
,得 ![]() ,
,
![]() .
.
![]() ,
,
![]() 当
当 ![]() 时,
时,![]() 的最大值为
的最大值为 ![]() .
.
![]() 即当
即当 ![]() 时,
时,![]() 的长最大,最大值是
的长最大,最大值是 ![]() ,
,
故答案为:![]() ,AB最大值是
,AB最大值是![]() .
.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案
相关题目