题目内容
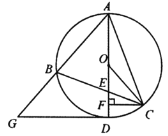
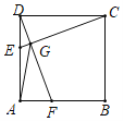
【题目】将两块全等的三角板如图①楔放,其中∠A'CB'=∠ACB=90°,∠A'=∠A=30°.

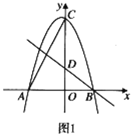
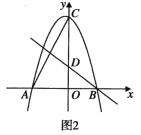
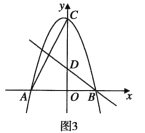
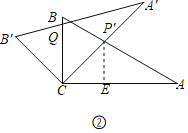
(1)将图①中的△A'B'C顺时针旋转45°得图②,点P'是A'C与AB的交点,点Q是A'B'与BC的交点,求证:CP'=CQ;
(2)在图②中,若AP'=3,求CQ长.
【答案】(1)详见解析;(2)![]()
【解析】
(1)由“ASA”可证△A′CQ≌△ACP′,可得CP′=CQ;
(2)由直角三角形的性质和全等三角形的性质可求CP′=CQ=![]() .
.
解:(1)∵将△A′B′C顺时针旋转45°,
∴∠ACA′=45°,AC=A′C,∠A=∠A′,
∵∠A′CB′=∠ACB=90°,
∴∠BCA′=∠ACA′=45°,且AC=A′C,∠A=∠A′,
∴△A′CQ≌△ACP′(ASA)
∴CP′=CQ;
(2)如图②,过点P′作P′E⊥AC,
∵∠A=30°,AP′=3,P′E⊥AC,
∴P′E=1.5,
∵∠ACA′=45°,P′E⊥AC,
∴CE=P′E=1.5,
∴P′C=![]() ,
,
∴CP′=CQ=![]() .
.

练习册系列答案
相关题目
【题目】有这样一个问题:探究函数![]() 的图象与性质.
的图象与性质.
文文根据学习函数的经验,对函数![]() 的图象与性质进行了探究.
的图象与性质进行了探究.
下面是文文的探究过程,请补充完整:
(1)函数![]() 的自变量x的取值范围是__________________;
的自变量x的取值范围是__________________;
(2)下表是y与x的几组对应值:
x | … |
|
|
|
|
| 0 |
| 1 |
| 2 | 3 | … |
y | … |
| 5 |
|
|
| 1 |
|
|
|
|
| … |
则m的值为____________;
(3)如图,在平面直角坐标系![]() 中,描出以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
中,描出以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
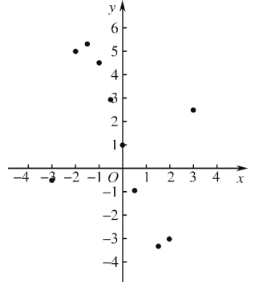
(4)请你根据探究二次函数与一元二次方程关系的经验,结合图象直接写出方程![]() 的正数根约为____________.(结果精确到0.1)
的正数根约为____________.(结果精确到0.1)