题目内容
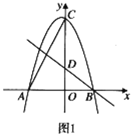
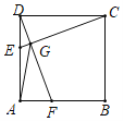
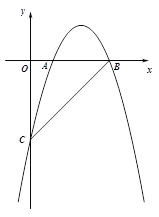
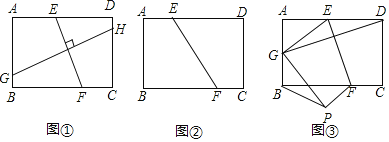
【题目】如图，在Rt△ABC中，∠C＝90°，AC＝2，BC＝4．点M1，N1，P1分别在AC，BC，AB上，且四边形M1CN1P1是正方形，点M2，N2，P2分别在P1N1，BN1，BP1上，且四边形M2N1N2P2是正方形，…，点Mn，Nn，Pn分别在Pn－1Nn－1，BNn－1，BPn－1上，且四边形MnNn－1NnPn是正方形，则线段BN2020的长度是__________．
【答案】
【解析】
设AM1的长为x，由题易得，△AM1P1∽△ACB，根据相似求得M1P1的长度，同理求得M2P2和MnPn，根据正方形的性质得P2020N2020=
，再由△P2020N2020B∽△ACB，对应边成比例求得BN2020．
设AM1的长为x，
由题易得，△AM1P1∽△ACB
∴
∵AC＝2，BC＝4
∴M1P1=2x，
∴AC= AM1+ M1P1=3x
∴x=
，AM1=，M1P1=
，
同理可得，M2P2=
，
MnPn=
∴M2020P2020=P2020N2020=
∵△P2020N2020B∽△ACB
∴
∴
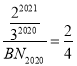
∴BN2020=
故答案为
【题目】某学校计划组织1200名师生参加社会实践活动，其中包括25名教师与某公交公司洽谈后得知该公司有A、B型两种客车．每辆A型客车载客54人，租金480元；每辆B型客车载客36人，租金280元．由于每辆车上要求有一名教师，决定租用25辆客车．
设租用A型客车x辆（x为非负整数）．
（Ⅰ）根据题意填写下表：
客车类型 | 车辆数（辆） | 载客数（人） | 租金（元） |
A型客车 | x | ||
B型客车 |
|
（Ⅱ）若租车总费用为10800元，怎样安排车辆？
（Ⅲ）采取怎样的租车方案可以使租车总费用最低，最低是多少元？
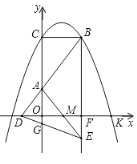
【题目】有这样一个问题：探究函数
的图象与性质．
文文根据学习函数的经验，对函数的图象与性质进行了探究．
下面是文文的探究过程，请补充完整：
（1）函数的自变量x的取值范围是__________________；
（2）下表是y与x的几组对应值：
x | … |
|
|
|
|
| 0 |
| 1 |
| 2 | 3 | … |
y | … |
| 5 |
|
|
| 1 |
|
|
|
|
| … |
则m的值为____________；
（3）如图，在平面直角坐标系
中，描出以上表中各对对应值为坐标的点．根据描出的点，画出该函数的图象；
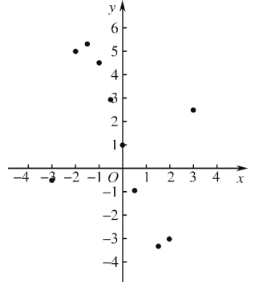
（4）请你根据探究二次函数与一元二次方程关系的经验，结合图象直接写出方程
的正数根约为____________．（结果精确到0.1）
