题目内容
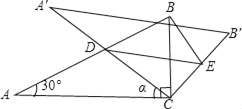
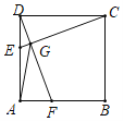
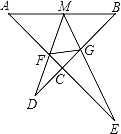
【题目】如图M为线段AB的中点,AE与BD交于点C,∠DME=∠A=∠B=45°,且DM交AC于F,ME交BC于G,连接FG,若AB=![]() ,AF=3,则BG=_____,FG=_____.
,AF=3,则BG=_____,FG=_____.
【答案】![]()
![]()
【解析】
由于∠DME=∠A=∠B=45![]() ,利用外角定理证得∠AFM=∠BMG,即可推出AMF∽△BGM,再根据相似三角形的性质,推出BG的长度,依据锐角三角函数推出AC的长度,即可求出CG、CF的长度,继而推出FG的长度.
,利用外角定理证得∠AFM=∠BMG,即可推出AMF∽△BGM,再根据相似三角形的性质,推出BG的长度,依据锐角三角函数推出AC的长度,即可求出CG、CF的长度,继而推出FG的长度.
∵∠DME=∠A=∠B=45°
∴AC=BC,∠ACB=90°,
∴AC⊥BC,
∵M为AB的中点,
∴AM=BM=2![]() ,
,
∵∠AFM=∠DME+∠E(外角定理),
∠DME=∠A=∠B(已知),
∴∠AFM=∠DME+∠E=∠A+∠E=∠BMG,∠A=∠B,
∴△AMF∽△BGM,
∴![]() ,
,
∴BG=![]() =
=![]() ,
,
AC=BC=4![]() cos45°=4,
cos45°=4,
∴CG=4﹣![]() =
=![]() ,CF=4﹣3=1,
,CF=4﹣3=1,
在Rt△FCG中,由勾股定理得:
FG=![]() =
=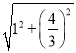 =
=![]() .
.
故答案为:![]() ,
,![]() .
.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
【题目】某学校计划组织1200名师生参加社会实践活动,其中包括25名教师与某公交公司洽谈后得知该公司有A、B型两种客车.每辆A型客车载客54人,租金480元;每辆B型客车载客36人,租金280元.由于每辆车上要求有一名教师,决定租用25辆客车.
设租用A型客车x辆(x为非负整数).
(Ⅰ)根据题意填写下表:
客车类型 | 车辆数(辆) | 载客数(人) | 租金(元) |
A型客车 | x | ||
B型客车 |
|
(Ⅱ)若租车总费用为10800元,怎样安排车辆?
(Ⅲ)采取怎样的租车方案可以使租车总费用最低,最低是多少元?