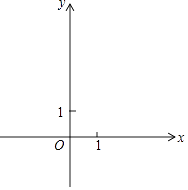题目内容
【题目】如图,在平面直角坐标系xOy中,抛物线y=﹣x2+bx+c经过点A(3,0)和点B(2,3),过点A的直线与y轴的负半轴相交于点C,且tan∠CAO= ![]() .
. 
(1)求这条抛物线的表达式及对称轴;
(2)联结AB、BC,求∠ABC的正切值;
(3)若点D在x轴下方的对称轴上,当S△DBC=S△ADC时,求点D的坐标.
【答案】
(1)解:把A(3,0)和点B(2,3)代入y=﹣x2+bx+c得到 ![]() ,
,
解得 ![]() ,
,
∴抛物线的解析式为y=﹣x2+2x+3,
对称轴x=1
(2)解:如图,作BE⊥OA于E.
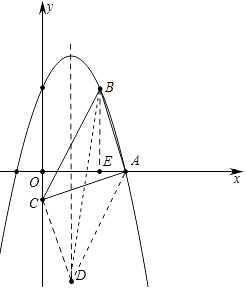
∵A(3,0),B(2,3),tan∠CAO= ![]() ,
,
∴OC=1,
∴BE=OA=3,AE=OC=1,∵AEB=∠AOC,
∴△AOC≌△BEA,
∴AC=AB,∠CAO=∠BAE,
∵∠ABE+∠BAE=90°,
∴∠CAO+∠BAE=90°,
∴∠CAB=90°,
∴△ABC是等腰直角三角形,
∴∠ABC=45°,
∴tan∠ABC=1
(3)解:如图过点C作CD∥AB交对称轴于D,

则S△DBC=S△ADC,
∵AB⊥AC,AB∥CD,
∴AC⊥CD,
∵直线AC的解析式为y= ![]() x﹣1,
x﹣1,
∴直线CD的解析式为y=﹣3x﹣1,当x=1时,y=﹣4,
∴点D的坐标为(1,﹣4).
【解析】(1)把A(3,0)和点B(2,3)代入y=﹣x2+bx+c,解方程组即可解决问题.(2)如图,作BE⊥OA于E.只要证明△AOC≌△BEA,推出△ABC是等腰直角三角形,即可解决问题.(3)如图过点C作CD∥AB交对称轴于D,则S△DBC=S△ADC , 先求出直线AC的解析式,再求出直线CD的解析式即可解决问题.
【考点精析】通过灵活运用抛物线与坐标轴的交点和解直角三角形,掌握一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.;解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法)即可以解答此题.