题目内容
【题目】如图,直线 AB,CD 相交于点O,OE 平分∠AOD,OF⊥OC.
(1)图中∠AOF 的余角是_____ _____(把符合条件的角都填出来);
(2)如果∠AOC=120°,那么根据____ ______,可得∠BOD=__________°;
(3)如果∠1=32°,求∠2和∠3的度数.
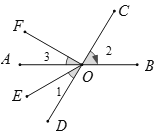
【答案】(1)∠AOD,∠BOC;(2)对顶角相等;120°;(3)∠2=64°,∠3=26°.
【解析】
(1)由垂线的定义和角的互余关系即可得出结果;
(2)由对顶角相等即可得出结果;
(3)由角平分线的定义求出∠AOD,由对顶角相等得出∠2的度数,再由角的互余关系即可求出∠3的度数.
(1)∵直线AB,CD相交于点O,
∴∠AOD=∠BOC
∵OF⊥OC
∴∠COF=90°
∴∠AOF+∠2=90°
∴∠AOF+∠AOD=90°
∠AOF的余角是∠2和∠AOD.即∠AOF的余角是∠BOC和∠AOD
(2)如果∠AOC=120°,那么根据对顶角相等可得∠BOD=120°
(3)∵OE平分∠AOD,∴∠AOD=2∠1=2×32°=64°
∴∠2=∠AOD=64°
∵∠COF=90°
∴∠3=90°-∠2=90°-64°=26°.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
【题目】某小区为了促进生活垃圾的分类处理,将生活垃圾分为:可回垃圾、厨余垃圾、其他垃圾三类,分别记为A,B,C:并且设置了相应的垃圾箱,依次记为a,b,c.
(1)若将三类垃圾随机投入三个垃圾箱,请你用树形图的方法求垃圾投放正确的概率:
(2)为了调查小区垃圾分类投放情况,现随机抽取了该小区三类垃圾箱中总重500kg生活垃圾,数据如下(单位:)
a | b | c | |
A | 40 | 15 | 10 |
B | 60 | 250 | 40 |
C | 15 | 15 | 55 |
试估计“厨余垃圾”投放正确的概率.