题目内容
【题目】已知△ABC与△ABD不全等,且AC=AD=1,∠ABD=∠ABC=45°,∠ACB=60°,则CD= .
【答案】1或![]() .
.
【解析】分析:
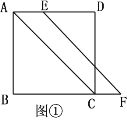
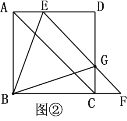
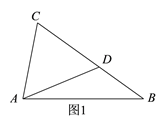
由题意可知本题存在两种可能情况:(1)如图1,C、D两点在线段AB的同侧,此时由已知条件易证△ACD是等边三角形,由此即可求得CD的长;(2)如图2,C、D两点在线段AB的两侧,此时由已知条件可知将△ABD沿AB翻折,点D的对应点D′刚好落在BC边上,连接CD,由已知条件可证得∠CAD=90°,从而可在Rt△ACD中由勾股定理求得CD的长.
详解:
(1)如图1,当C、D在AB同侧时,
∵AC=AD=1,∠C=60°,
∴△ACD是等边三角形,
∴CD=AC=1;
(2)如图2,当C、D在AB两侧时,
∵∠ABC=∠ABD=45°,
∴把△ABD沿AB翻折得到△ABD′时,点D′在BC边上,
由(1)可知,此时△ACD′是等边三角形,
∴∠AD′C=60°,
∴∠AD′B=120°,
∴∠ADB=120°,
又∵在四边形ADBC中,∠ACB=60°,∠DBC=∠ABC+∠ABD=90°,
∴∠CAD=360°-60°-120°-90°=90°,
∴在Rt△ACD中,CD=![]() .
.

综上所述可得CD的长为1或![]() .
.
故答案为:1或![]() .
.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目