Question

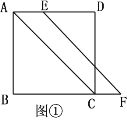
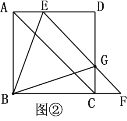
【题目】已知,在正方形ABCD中,点E在边AD上,点F在边BC的延长线上,且AE=CF,连接AC，EF.

(1)如图①,求证：EF//AC；

(2)如图②,EF与边CD交于点G,连接BG,BE,

①求证:△BAE≌△BCG;

②若BE=EG=4,求△BAE的面积.

Answer 1

【答案】（1）见解析；（2）①见解析；②△BAE的面积为2.

【解析】

（1）利用平行四边形的判定及其性质定理即可解决问题；

（2）①根据SAS可以证明两三角形全等；

②先根据等腰直角△DEG计算DE的长，设AE=a，表示正方形的边长，根据勾股定理列式，可得+a=4，最后根据三角形面积公式，整体代入可得结论．

（1）证明：∵正方形ABCD

∴AE//CF，

∵AE=CF

∴AEFC是平行四边形

∴EF//AC.

（2）①如图，

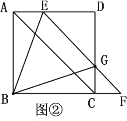
∵四边形ABCD是正方形，且EF∥AC，

∴∠DEG=∠DAC=45°，∠DGE=∠DCA=45°；

∵AD∥BF，

∴∠CFG=∠DEG=45°，

∵∠CGF=∠DGE=45°，

∴∠CGF=∠CFG，

∴CG=CF；

∵AE=CF，

∴AE=CG；

在△ABE与△CBG中，

∵AE=CG，∠BAE=∠BCG，AB=BC

∴△ABE≌CBG（SAS）；

②由①知△DEG是等腰直角三角形，

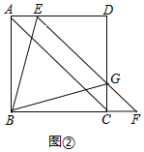
∵EG=4，

∴DE=，

设AE=a，则AB=AD=a+，

Rt△ABE中，由勾股定理得：AB2+AE2=BE2，

∴(a+)2+a2=42，

∴a2+a=4，

∴S△ABE=ABAE=a(a+)= (a2+a)=×4=2．