题目内容
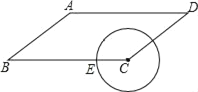
【题目】如图，已知在平行四边形ABCD中，AB=5，BC=8，cosB=
，点E是BC边上的动点，当以CE为半径的⊙C与边AD有两个交点时，半径CE的取值范围是（ ）
A. 0＜CE≤8 B. 0＜CE≤5 C. 3＜CE≤8 D. 3＜CE≤5
【答案】D
【解析】
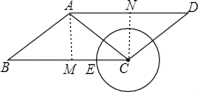
过A作AM⊥BC于N，CN⊥AD于N，由平行四边形的性质可知AD∥BC，AB=CD=5，求出AM，CN，AC，CD的长，即可得出符合条件的结论.
如图，过A作AM⊥BC于N，CN⊥AD于N，
∵四边形ABCD是平行四边形，
∴AD∥BC，AB=CD=5，
∴AM=CN，
∵AB=5，cosB=
=
，
∴BM=4，
∵BC=8，
∴CM=4=BC，
∵AM⊥BC，
∴AC=AB=5，
由勾股定理得：AM=CN=
=3，
∴当以CE为半径的圆C与边AD有两个交点时，半径CE的取值范围是3＜CE≤5，
故选：D．
练习册系列答案
相关题目
