题目内容
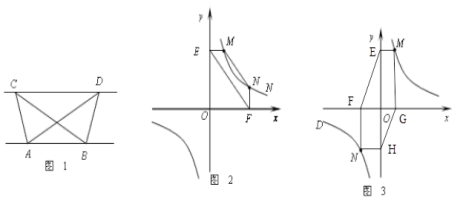
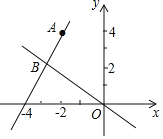
【题目】如图，在平面直角坐标系xOy中，一次函y=kx+b的图象经过点A（-2，4），且与正比例函数
的图象交于点B（a，2）．
（1）求a的值及一次函数y=kx+b的解析式；
（2）若一次函数y=kx+b的图象与x轴交于点C，且正比例函数y=-
x的图象向下平移m（m＞0）个单位长度后经过点C，求m的值；
（3）直接写出关于x的不等式0＜
＜kx+b的解集．
【答案】（1）y=2x+8；（2）m=
；（3）-3＜x＜0
【解析】
（1）先确定B的坐标，然后根据待定系数法求解析式；
（2）先求得C的坐标，然后根据题意求得平移后的直线的解析式，把C的坐标代入平移后的直线的解析式，即可求得M的值；
（3）找出直线y=-
x落在y=kx+b的下方且在x轴上方的部分对应的x的取值范围即可．
解：（1）∵正比例函数
的图象经过点B（a，2），
∴2=-a，解得，a=-3，
∴B（-3，2），
∵一次函数y=kx+b的图象经过点A（-2，4），B（-3，2），
∴
，解得
，
∴一次函数y=kx+b的解析式为y=2x+8；
（2）∵一次函数y=2x+8的图象与x轴交于点C，
∴C（-4，0），
∵正比例函数y=-x的图象向下平移m（m＞0）个单位长度后经过点C，
∴平移后的函数的解析式为y=-x-m，
∴0=-×（-4）-m，
解得m=；
（3）∵一次函y=kx+b与正比例函数y=-x的图象交于点B（-3，2），
且一次函数y=2x+8的图象与x轴交于点C（-4，0），
∴关于x的不等式0＜-x＜kx+b的解集是-3＜x＜0．
备战中考寒假系列答案
【题目】某公司需招聘一名员工，对应聘者甲、乙、丙从笔试、面试、体能三个方面进行量化考核．甲、乙、丙各项得分如下表：
笔 试 | 面 试 | 体 能 | |
甲 | 85 | 80 | 75 |
乙 | 80 | 90 | 73 |
丙 | 83 | 79 | 90 |
（1）根据三项得分的平均分，从高到低确定三名应聘者的排名顺序．
（2）该公司规定：笔试，面试、体能得分分别不得低于80分，80分，70分，并按60%，30%，10%的比例计入总分（不计其他因素条件），请你说明谁将被录用．
