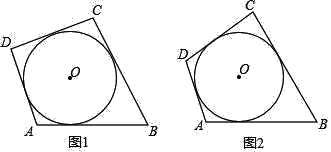题目内容
【题目】问题发现:
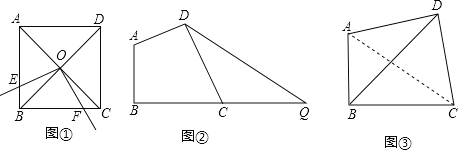
(1)如图①,正方形ABCD的边长为4,对角线AC、BD相交于点O,E是AB上点(点E不与A、B重合),将射线OE绕点O逆时针旋转90°,所得射线与BC交于点F,则四边形OEBF的面积为 .
问题探究:
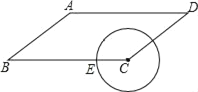
(2)如图②,线段BQ=10,C为BQ上点,在BQ上方作四边形ABCD,使∠ABC=∠ADC=90°,且AD=CD,连接DQ,求DQ的最小值;
问题解决:
(3)“绿水青山就是金山银山”,某市在生态治理活动中新建了一处南山植物园,图③为南山植物园花卉展示区的部分平面示意图,在四边形ABCD中,∠ABC=∠ADC=90°,AD=CD,AC=600米.其中AB、BD、BC为观赏小路,设计人员考虑到为分散人流和便观赏,提出三条小路的长度和要取得最大,试求AB+BD+BC的最大值.
【答案】(1)4;(2)5![]() ;(3)600(
;(3)600(![]() +1).
+1).
【解析】
(1)如图①中,证明△EOB≌△FOC即可解决问题;
(2)如图②中,连接BD,取AC的中点O,连接OB,OD.利用四点共圆,证明∠DBQ=∠DAC=45°,再根据垂线段最短即可解决问题.
(3)如图③中,将△BDC绕点D顺时针旋转90°得到△EDA,首先证明AB+BC+BD=(![]() +1)BD,当BD最大时,AB+BC+BD的值最大.
+1)BD,当BD最大时,AB+BC+BD的值最大.
解:(1)如图①中,
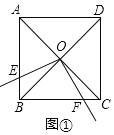
∵四边形ABCD是正方形,
∴OB=OC,∠OBE=∠OCF=45°,∠BOC=90°,
∵∠EOF=90°,
∴∠EOF=∠BOC,
∴∠EOB=∠FOC,
∴△EOB≌△FOC(SAS),
∴S△EOB=S△OFC,
∴S四边形OEBF=S△OBC=![]() S正方形ABCD=4,
S正方形ABCD=4,
故答案为:4;
(2)如图②中,连接BD,取AC的中点O,连接OB,OD.
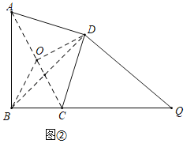
∵∠ABD=∠ADC=90°,AO=OC,
∴OA=OC=OB=OD,
∴A,B,C,D四点共圆,
∴∠DBC=∠DAC,
∵DA=DC,∠ADC=90°,
∴∠DAC=∠DCA=45°,
∴∠DBQ=45°,
根据垂线段最短可知,当QD⊥BD时,QD的值最短,DQ的最小值=![]() BQ=5
BQ=5![]() .
.
(3)如图③中,将△BDC绕点D顺时针旋转90°得到△EDA,
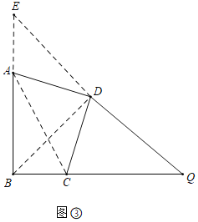
∵∠ABC+∠ADC=180°,
∴∠BCD+∠BAD=∠EAD+BAD=180°,
∴B,A,E三点共线,
∵DE=DB,∠EDB=90°,
∴BE=![]() BD,
BD,
∴AB+BC=AB+AE=BE=![]() BD,
BD,
∴BC+BC+BD=(![]() +1)BD,
+1)BD,
∴当BD最大时,AB+BC+BD的值最大,
∵A,B,C,D四点共圆,
∴当BD为直径时,BD的值最大,
∵∠ADC=90°,
∴AC是直径,
∴BD=AC时,AB+BC+BD的值最大,最大值=600(![]() +1).
+1).

【题目】某校团委举办了一次“中国梦我的梦”演讲比赛满分10分,学生得分均为整数,成绩达6分以上(含6分)为合格,达到9分以上(含9分)为优秀.如图所示是这次竞赛中甲、乙两组学生成绩分布的条形统计图.
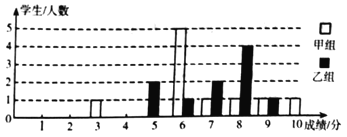
(1)补充完成下列的成绩统计分析表:
组别 | 平均分 | 中位数 | 方差 | 合格率 | 优秀率 |
甲 | 6 | 3.41 | 90% | 20% | |
乙 | 7.1 | 1.69 | 80% | 10% |
(2)小明同学说:“这次竞赛我得了7分,在我们小组中排名属中游略偏上!”观察上表可知,小明是______组学生;(填“甲”或“乙”)
(3)甲组同学说他们组的合格率、优秀率均高于乙组,所以他们组的成绩好于乙组.但乙组同学不同意甲组同学的说法,认为他们组的成绩要好于甲组.请你给出两条支持乙组同学观点的理由.