题目内容
【题目】作图题(不写作法,保留作图痕迹)
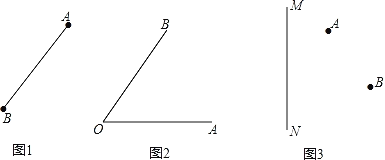
(1)如图1请利用直尺和圆规作线段AB的中垂线EF;
(2)如图2请利用直尺和圆规作∠AOB的角平分线OC;
(3)如图3,要在公路MN上修一个车站P,使得P向AB两个地方的距离和最小,请利用直尺和圆规画出P的位置;
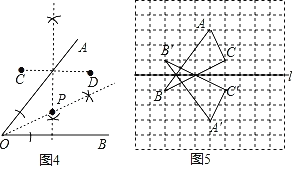
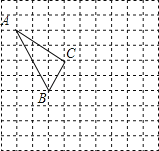
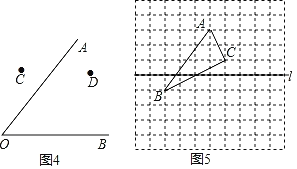
(4)如图4,已知∠AOB及点C、D两点,请利用直尺和圆规作一点P,使得点P到射线OA、OB的距离相等,且P点到点C、D的距离也相等;
(5)如图5,利用网状格画出△ABC关于直线l的对称图形△A'B'C'.
【答案】(1)如图1,直线EF为所作;见解析;(2)如图2,射线OC为所作;见解析;(3)如图3,点P为所作;见解析;(4)如图4,点P为所作;见解析;(5)如图5,△A′B′C′为所作.见解析.
【解析】
(1)利用基本作图,作线段AB的垂直平分线得到直线EF;
(2)利用基本作图,作OC平分;
(3)作A点关于MN的对称点A′,连接BA′交MN于P,利用两点之间线段最短可判断P点满足条件;
(4)作线段CD的垂直平分线和∠AOB的平分线,它们相交于点P,则点P满足条件;
(5)利用网格特点和对称的性质分别画出A、B、C的对称点A′、B′、C′即可.
(1)如图1,分别以点A和点B为圆心,以任意长为半径画弧,两弧相较于E、F两点,连接E、F两点,直线EF为所作;
(2)如图2,以点O为圆心,任意长为半径画弧,交∠AOB于两点G、H,再以两交点为圆心,大于![]() GH的长为半径画弧,两弧交于一点C,连接OC,射线OC为所作;
GH的长为半径画弧,两弧交于一点C,连接OC,射线OC为所作;
(3)如图3,作A点关于MN的对称点A′,连接BA′交MN于P,点P为所作;
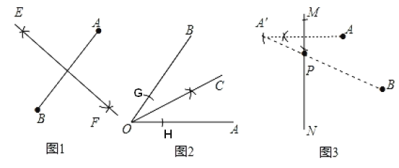
(4)如图4,作线段CD的垂直平分线和∠AOB的平分线,它们相交于点P,点P为所作;
(5)如图5,利用网格特点和对称的性质分别画出A、B、C的对称点A′、B′、C′,顺次连接点A′、B′、C′,△A′B′C′为所作.