题目内容
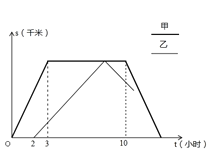
【题目】综合实践课上,某小组同学将直角三角形纸片放到横线纸上(所有横线都平行,且相邻两条平行线的距离为1),使直角三角形纸片的顶点恰巧在横线上,发现这样能求出三角形的边长.
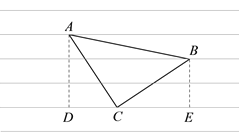
(1)如图1,已知等腰直角三角形纸片△ABC,∠ACB=90°,AC=BC,同学们通过构造直角三角形的办法求出三角形三边的长,则AB=__________;

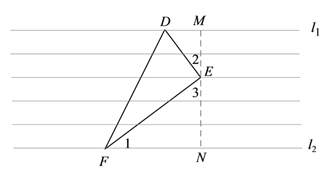
(2)如图2,已知直角三角形纸片△DEF,∠DEF=90°,EF=2DE,求出DF的长;

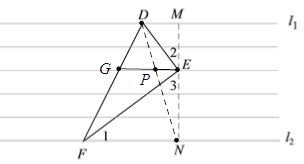
(3)在(2)的条件下,若橫格纸上过点E的横线与DF相交于点G,直接写出EG的长.
【答案】AB=![]() ;
;
【解析】试题分析:(1)如图,过点A、B分别作点C所在横线的垂线,垂足分别为D、E,然后证明△ADC≌△CEB,从而可得CE=AD=3,CD=BE=2,由勾股定理求得AC,BC的长,再由勾股定理即可求得AB的长;
(2)如图所示,过点E作横线的垂线,然后证明△DME∽△ENF,再根据相似三角形的性质进行推导即可得;
(3)连接DN与EG交于点P,根据相似三角形的性质即可得.
试题解析:(1)过点A、B分别作点C所在横线的垂线,垂足分别为D、E,
∴∠ADC=∠BEC=90°,AD=3,BE=2,
∴∠DAC+∠ACD=90°,
∵∠ACB=90°,∴∠ACD+∠BCE=90°,
∴∠DAC=∠ECB,
∵AC=BC,
∴△ADC≌△CEB,∴CE=AD=3,CD=BE=2,
∴AC=BC=![]() ,∴AB=
,∴AB=![]() ,
,
故答案为: ![]() ;
;
(2)过点E作横线的垂线,交l1,l2于点M,N,
∴∠DME=∠EDF= 90°,
∵∠DEF=90°,
∴∠2+∠3=90°,
∵∠1+∠3=90°,
∴∠1=∠2,
∴△DME∽△ENF ,
∴![]() ,
,
∵EF=2DE,
∴![]() ,
,
∵ME=2,EN=3,
∴NF=4,DM=1.5,
根据勾股定理得DE=2.5,EF=5, ![]() ;
;
(3)连接DN,交EG于点P,
∵EG//DM,∴△DMN∽△PEN,
∴PE:DM=EN:MN,即PE:1.5=3:5,∴PE=0.9,
同理PG=1.6,∴EG=PE+PG=2.5.

 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案